↑

Properties

Label 2-39e2-13.2-c0-0-3
Degree $2$
Conductor $1521$
Sign $0.999 - 0.0386i$
Analytic cond. $0.759077$
Root an. cond. $0.871250$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

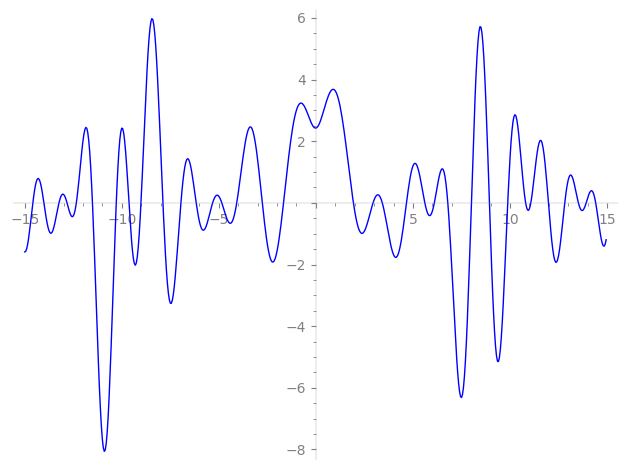
L(s)  = 1  + (1.36 + 0.366i)2-s + (0.866 + 0.5i)4-s + (1 − i)5-s + (1.73 − i)10-s + (−0.366 + 1.36i)11-s + (−0.499 − 0.866i)16-s + (1.36 − 0.366i)20-s + (−1 + 1.73i)22-s − i·25-s + (−0.366 − 1.36i)32-s + (−1.36 − 0.366i)41-s + (1.73 + i)43-s + (−1 + 0.999i)44-s + (−1 − i)47-s + (−0.866 + 0.5i)49-s + (0.366 − 1.36i)50-s + ⋯
L(s)  = 1  + (1.36 + 0.366i)2-s + (0.866 + 0.5i)4-s + (1 − i)5-s + (1.73 − i)10-s + (−0.366 + 1.36i)11-s + (−0.499 − 0.866i)16-s + (1.36 − 0.366i)20-s + (−1 + 1.73i)22-s − i·25-s + (−0.366 − 1.36i)32-s + (−1.36 − 0.366i)41-s + (1.73 + i)43-s + (−1 + 0.999i)44-s + (−1 − i)47-s + (−0.866 + 0.5i)49-s + (0.366 − 1.36i)50-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1521 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.999 - 0.0386i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1521 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.999 - 0.0386i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(1521\)    =    \(3^{2} \cdot 13^{2}\)
Sign: $0.999 - 0.0386i$
Analytic conductor: \(0.759077\)
Root analytic conductor: \(0.871250\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{1521} (1432, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 1521,\ (\ :0),\ 0.999 - 0.0386i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(2.427140141\)
\(L(\frac12)\) \(\approx\) \(2.427140141\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad3 \( 1 \)
13 \( 1 \)
good2 \( 1 + (-1.36 - 0.366i)T + (0.866 + 0.5i)T^{2} \)
5 \( 1 + (-1 + i)T - iT^{2} \)
7 \( 1 + (0.866 - 0.5i)T^{2} \)
11 \( 1 + (0.366 - 1.36i)T + (-0.866 - 0.5i)T^{2} \)
17 \( 1 + (0.5 + 0.866i)T^{2} \)
19 \( 1 + (-0.866 + 0.5i)T^{2} \)
23 \( 1 + (0.5 - 0.866i)T^{2} \)
29 \( 1 + (-0.5 + 0.866i)T^{2} \)
31 \( 1 - iT^{2} \)
37 \( 1 + (-0.866 - 0.5i)T^{2} \)
41 \( 1 + (1.36 + 0.366i)T + (0.866 + 0.5i)T^{2} \)
43 \( 1 + (-1.73 - i)T + (0.5 + 0.866i)T^{2} \)
47 \( 1 + (1 + i)T + iT^{2} \)
53 \( 1 + T^{2} \)
59 \( 1 + (1.36 - 0.366i)T + (0.866 - 0.5i)T^{2} \)
61 \( 1 + (-0.5 - 0.866i)T^{2} \)
67 \( 1 + (0.866 + 0.5i)T^{2} \)
71 \( 1 + (-0.366 - 1.36i)T + (-0.866 + 0.5i)T^{2} \)
73 \( 1 + iT^{2} \)
79 \( 1 + T^{2} \)
83 \( 1 + (1 - i)T - iT^{2} \)
89 \( 1 + (-0.366 + 1.36i)T + (-0.866 - 0.5i)T^{2} \)
97 \( 1 + (-0.866 + 0.5i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−9.627295815795258291399525624070, −9.010093944693941763344673284335, −7.87894053040409549726745463023, −6.95226163330634574248551785687, −6.16528671611276756694382475602, −5.31946055384630044631537323867, −4.84672972981776856958144039799, −4.07800100687861798798968593928, −2.75928812159246748507520268650, −1.66788522944546560811375725694, 1.93216772732673882481633639646, 2.94371747653891445625218477173, 3.41862342013857292150232990428, 4.66548507964020217502891770608, 5.61110077237492478153073272798, 6.10024487046170048702413973472, 6.79381963602542819335994620996, 8.009555252667046027492794295819, 8.937656671001005100145853633412, 9.880872982848770537550837972148

Graph of the $Z$-function along the critical line