↑

Properties

Label 2-448-448.349-c0-0-0
Degree $2$
Conductor $448$
Sign $-0.290 - 0.956i$
Analytic cond. $0.223581$
Root an. cond. $0.472843$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.382 + 0.923i)2-s + (−0.707 + 0.707i)4-s + (−0.923 + 0.382i)7-s + (−0.923 − 0.382i)8-s + (0.923 + 0.382i)9-s + (0.324 + 1.63i)11-s + (−0.707 − 0.707i)14-s − i·16-s + i·18-s + (−1.38 + 0.923i)22-s + (0.707 − 1.70i)23-s + (−0.382 − 0.923i)25-s + (0.382 − 0.923i)28-s + (0.216 − 1.08i)29-s + (0.923 − 0.382i)32-s + ⋯
L(s)  = 1  + (0.382 + 0.923i)2-s + (−0.707 + 0.707i)4-s + (−0.923 + 0.382i)7-s + (−0.923 − 0.382i)8-s + (0.923 + 0.382i)9-s + (0.324 + 1.63i)11-s + (−0.707 − 0.707i)14-s − i·16-s + i·18-s + (−1.38 + 0.923i)22-s + (0.707 − 1.70i)23-s + (−0.382 − 0.923i)25-s + (0.382 − 0.923i)28-s + (0.216 − 1.08i)29-s + (0.923 − 0.382i)32-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 448 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.290 - 0.956i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 448 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.290 - 0.956i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(448\)    =    \(2^{6} \cdot 7\)
Sign: $-0.290 - 0.956i$
Analytic conductor: \(0.223581\)
Root analytic conductor: \(0.472843\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{448} (349, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 448,\ (\ :0),\ -0.290 - 0.956i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.9153627997\)
\(L(\frac12)\) \(\approx\) \(0.9153627997\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (-0.382 - 0.923i)T \)
7 \( 1 + (0.923 - 0.382i)T \)
good3 \( 1 + (-0.923 - 0.382i)T^{2} \)
5 \( 1 + (0.382 + 0.923i)T^{2} \)
11 \( 1 + (-0.324 - 1.63i)T + (-0.923 + 0.382i)T^{2} \)
13 \( 1 + (0.382 - 0.923i)T^{2} \)
17 \( 1 - iT^{2} \)
19 \( 1 + (-0.382 + 0.923i)T^{2} \)
23 \( 1 + (-0.707 + 1.70i)T + (-0.707 - 0.707i)T^{2} \)
29 \( 1 + (-0.216 + 1.08i)T + (-0.923 - 0.382i)T^{2} \)
31 \( 1 + T^{2} \)
37 \( 1 + (0.324 + 0.216i)T + (0.382 + 0.923i)T^{2} \)
41 \( 1 + (0.707 + 0.707i)T^{2} \)
43 \( 1 + (0.382 - 0.0761i)T + (0.923 - 0.382i)T^{2} \)
47 \( 1 - iT^{2} \)
53 \( 1 + (-0.382 - 1.92i)T + (-0.923 + 0.382i)T^{2} \)
59 \( 1 + (0.382 + 0.923i)T^{2} \)
61 \( 1 + (-0.923 - 0.382i)T^{2} \)
67 \( 1 + (1.92 + 0.382i)T + (0.923 + 0.382i)T^{2} \)
71 \( 1 + (-1.30 + 0.541i)T + (0.707 - 0.707i)T^{2} \)
73 \( 1 + (-0.707 - 0.707i)T^{2} \)
79 \( 1 + (0.541 - 0.541i)T - iT^{2} \)
83 \( 1 + (-0.382 + 0.923i)T^{2} \)
89 \( 1 + (0.707 - 0.707i)T^{2} \)
97 \( 1 + T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

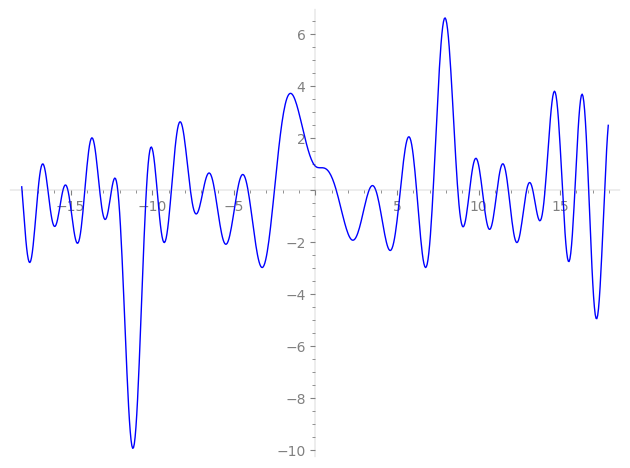
Imaginary part of the first few zeros on the critical line

−12.11639916572497631634618615686, −10.35975306681417962045267137553, −9.703128394198623611340275720439, −8.827714643004513568855999051045, −7.66380835195516936024913954204, −6.87535110408835168306397938790, −6.18073434917292392613427763235, −4.77629470737715626755322504908, −4.13307241291556885672749716365, −2.51143894717075304928801970058, 1.27416153341040169943284816662, 3.29279849857578592394624745439, 3.69589403950151495664122088322, 5.20708169082076706543131504249, 6.20107513393605711136734091612, 7.21785965465829034292177828359, 8.726505306528812413204516739893, 9.451934533169859489030986156027, 10.22517330402765310952347166300, 11.13514997682342806357188859709

Graph of the $Z$-function along the critical line