↑

Properties

Label 2-504-168.83-c0-0-0
Degree $2$
Conductor $504$
Sign $0.985 - 0.169i$
Analytic cond. $0.251528$
Root an. cond. $0.501526$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

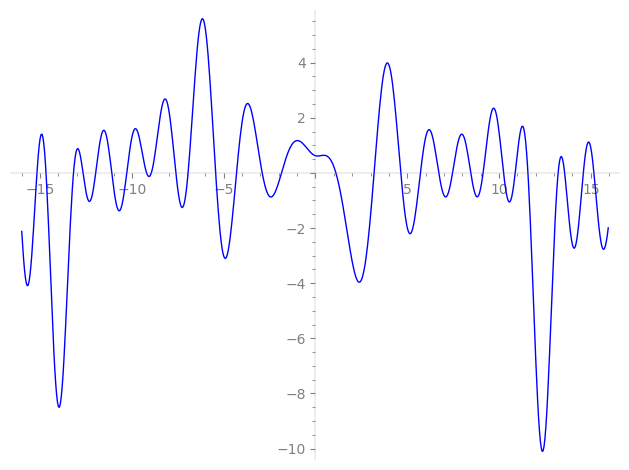
L(s)  = 1  + (−0.707 − 0.707i)2-s + 1.00i·4-s + i·7-s + (0.707 − 0.707i)8-s + 1.41i·11-s + (0.707 − 0.707i)14-s − 1.00·16-s + (1.00 − 1.00i)22-s + 1.41·23-s + 25-s − 1.00·28-s − 1.41·29-s + (0.707 + 0.707i)32-s − 2i·37-s − 1.41·44-s + ⋯
L(s)  = 1  + (−0.707 − 0.707i)2-s + 1.00i·4-s + i·7-s + (0.707 − 0.707i)8-s + 1.41i·11-s + (0.707 − 0.707i)14-s − 1.00·16-s + (1.00 − 1.00i)22-s + 1.41·23-s + 25-s − 1.00·28-s − 1.41·29-s + (0.707 + 0.707i)32-s − 2i·37-s − 1.41·44-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 504 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.985 - 0.169i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 504 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.985 - 0.169i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(504\)    =    \(2^{3} \cdot 3^{2} \cdot 7\)
Sign: $0.985 - 0.169i$
Analytic conductor: \(0.251528\)
Root analytic conductor: \(0.501526\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{504} (251, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 504,\ (\ :0),\ 0.985 - 0.169i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.6237091526\)
\(L(\frac12)\) \(\approx\) \(0.6237091526\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (0.707 + 0.707i)T \)
3 \( 1 \)
7 \( 1 - iT \)
good5 \( 1 - T^{2} \)
11 \( 1 - 1.41iT - T^{2} \)
13 \( 1 + T^{2} \)
17 \( 1 + T^{2} \)
19 \( 1 - T^{2} \)
23 \( 1 - 1.41T + T^{2} \)
29 \( 1 + 1.41T + T^{2} \)
31 \( 1 + T^{2} \)
37 \( 1 + 2iT - T^{2} \)
41 \( 1 + T^{2} \)
43 \( 1 + T^{2} \)
47 \( 1 - T^{2} \)
53 \( 1 - 1.41T + T^{2} \)
59 \( 1 + T^{2} \)
61 \( 1 + T^{2} \)
67 \( 1 + 2T + T^{2} \)
71 \( 1 + 1.41T + T^{2} \)
73 \( 1 - T^{2} \)
79 \( 1 - T^{2} \)
83 \( 1 + T^{2} \)
89 \( 1 + T^{2} \)
97 \( 1 - T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−11.09539624586277659311996316471, −10.27870536891162848238623005228, −9.197864045091260941480818990380, −8.941340081773811902399468238072, −7.60283446408897253793407365398, −6.93857146686148557311978969589, −5.43651881898298964296186649520, −4.29975263480637199568527049795, −2.90218956359490018053606238543, −1.84942642359722108302307649016, 1.11445972173035772105677404368, 3.19400757901157965243347857499, 4.64821740335521403509026352187, 5.71774425844654779051650892619, 6.71996813128602617644230951416, 7.46626462789162949627407698407, 8.461477255022252256962400027852, 9.131272453075463139142778115489, 10.24724136289547206026891892779, 10.88108714208982667795883332981

Graph of the $Z$-function along the critical line