↑

Properties

Label 2-580-580.419-c0-0-1
Degree $2$
Conductor $580$
Sign $0.441 - 0.897i$
Analytic cond. $0.289457$
Root an. cond. $0.538012$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

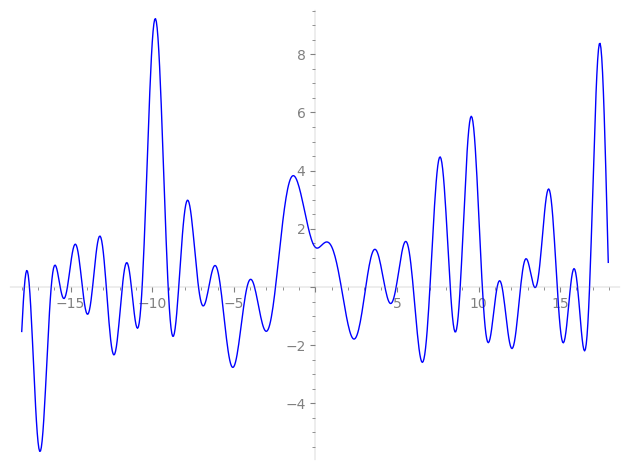
L(s)  = 1  + (0.900 + 0.433i)2-s + (0.623 + 0.781i)4-s + (−0.623 + 0.781i)5-s + (0.222 + 0.974i)8-s + (−0.222 − 0.974i)9-s + (−0.900 + 0.433i)10-s + (1.52 + 0.347i)13-s + (−0.222 + 0.974i)16-s − 1.80·17-s + (0.222 − 0.974i)18-s − 20-s + (−0.222 − 0.974i)25-s + (1.22 + 0.974i)26-s + (0.222 − 0.974i)29-s + (−0.623 + 0.781i)32-s + ⋯
L(s)  = 1  + (0.900 + 0.433i)2-s + (0.623 + 0.781i)4-s + (−0.623 + 0.781i)5-s + (0.222 + 0.974i)8-s + (−0.222 − 0.974i)9-s + (−0.900 + 0.433i)10-s + (1.52 + 0.347i)13-s + (−0.222 + 0.974i)16-s − 1.80·17-s + (0.222 − 0.974i)18-s − 20-s + (−0.222 − 0.974i)25-s + (1.22 + 0.974i)26-s + (0.222 − 0.974i)29-s + (−0.623 + 0.781i)32-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 580 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.441 - 0.897i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 580 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.441 - 0.897i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(580\)    =    \(2^{2} \cdot 5 \cdot 29\)
Sign: $0.441 - 0.897i$
Analytic conductor: \(0.289457\)
Root analytic conductor: \(0.538012\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{580} (419, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 580,\ (\ :0),\ 0.441 - 0.897i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.362599933\)
\(L(\frac12)\) \(\approx\) \(1.362599933\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (-0.900 - 0.433i)T \)
5 \( 1 + (0.623 - 0.781i)T \)
29 \( 1 + (-0.222 + 0.974i)T \)
good3 \( 1 + (0.222 + 0.974i)T^{2} \)
7 \( 1 + (-0.222 - 0.974i)T^{2} \)
11 \( 1 + (-0.900 - 0.433i)T^{2} \)
13 \( 1 + (-1.52 - 0.347i)T + (0.900 + 0.433i)T^{2} \)
17 \( 1 + 1.80T + T^{2} \)
19 \( 1 + (-0.222 + 0.974i)T^{2} \)
23 \( 1 + (0.623 - 0.781i)T^{2} \)
31 \( 1 + (0.623 + 0.781i)T^{2} \)
37 \( 1 + (0.277 + 1.21i)T + (-0.900 + 0.433i)T^{2} \)
41 \( 1 + 1.56iT - T^{2} \)
43 \( 1 + (-0.623 + 0.781i)T^{2} \)
47 \( 1 + (0.900 + 0.433i)T^{2} \)
53 \( 1 + (-0.376 + 0.781i)T + (-0.623 - 0.781i)T^{2} \)
59 \( 1 - T^{2} \)
61 \( 1 + (-0.678 - 0.541i)T + (0.222 + 0.974i)T^{2} \)
67 \( 1 + (-0.900 + 0.433i)T^{2} \)
71 \( 1 + (0.900 + 0.433i)T^{2} \)
73 \( 1 + (1.62 - 0.781i)T + (0.623 - 0.781i)T^{2} \)
79 \( 1 + (-0.900 + 0.433i)T^{2} \)
83 \( 1 + (-0.222 + 0.974i)T^{2} \)
89 \( 1 + (0.846 - 1.75i)T + (-0.623 - 0.781i)T^{2} \)
97 \( 1 + (0.777 + 0.974i)T + (-0.222 + 0.974i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−11.27873439430746192122302912146, −10.62118702019868772747839513774, −9.024579680535958772797008644967, −8.378320428893708805035660713849, −7.16454371891961185441362571337, −6.53334019678693129820153839089, −5.81537489412941952641311170558, −4.18998801268479225140940596260, −3.73171193255862131468476489472, −2.44541356668335301913385293995, 1.58495374033259793645313059458, 3.08542149507336186641921875867, 4.26101103228687722074456990902, 4.94891266858901709766676690871, 5.99338433081824304233099100540, 7.02138907511285923519816626893, 8.264112197088242833604015494002, 8.876312980051317415787712305591, 10.23078249620950821145710743450, 11.14051118176512432148844924560

Graph of the $Z$-function along the critical line