↑

Properties

Label 2-60-15.2-c1-0-1
Degree 22
Conductor 6060
Sign 0.794+0.607i0.794 + 0.607i
Analytic cond. 0.4791020.479102
Root an. cond. 0.6921720.692172
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

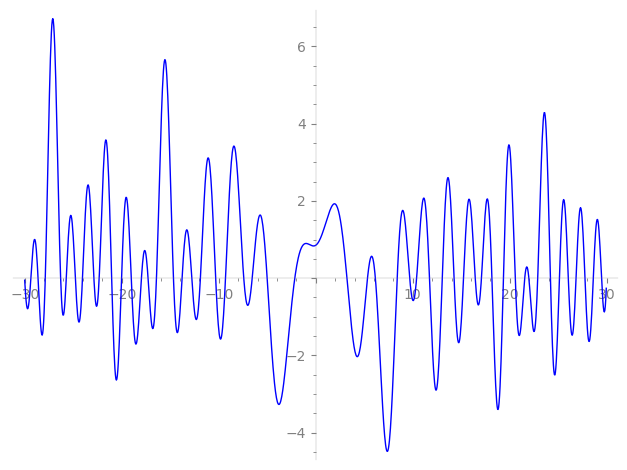
L(s)  = 1  + (−0.618 − 1.61i)3-s + 2.23·5-s + (−1 − i)7-s + (−2.23 + 2.00i)9-s + 4.47i·11-s + (−3 + 3i)13-s + (−1.38 − 3.61i)15-s + (2.23 − 2.23i)17-s − 2i·19-s + (−1 + 2.23i)21-s + (−2.23 − 2.23i)23-s + 5.00·25-s + (4.61 + 2.38i)27-s − 4.47·29-s + 4·31-s + ⋯
L(s)  = 1  + (−0.356 − 0.934i)3-s + 0.999·5-s + (−0.377 − 0.377i)7-s + (−0.745 + 0.666i)9-s + 1.34i·11-s + (−0.832 + 0.832i)13-s + (−0.356 − 0.934i)15-s + (0.542 − 0.542i)17-s − 0.458i·19-s + (−0.218 + 0.487i)21-s + (−0.466 − 0.466i)23-s + 1.00·25-s + (0.888 + 0.458i)27-s − 0.830·29-s + 0.718·31-s + ⋯

Functional equation

Λ(s)=(60s/2 ΓC(s) L(s)=((0.794+0.607i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 60 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.794 + 0.607i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(60s/2 ΓC(s+1/2) L(s)=((0.794+0.607i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 60 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.794 + 0.607i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 6060    =    22⋅3⋅52^{2} \cdot 3 \cdot 5
Sign: 0.794+0.607i0.794 + 0.607i
Analytic conductor: 0.4791020.479102
Root analytic conductor: 0.6921720.692172
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ60(17,⋅)\chi_{60} (17, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 60, ( :1/2), 0.794+0.607i)(2,\ 60,\ (\ :1/2),\ 0.794 + 0.607i)

Particular Values

L(1)L(1) ≈\approx 0.806615−0.272846i0.806615 - 0.272846i
L(12)L(\frac12) ≈\approx 0.806615−0.272846i0.806615 - 0.272846i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
3 1+(0.618+1.61i)T 1 + (0.618 + 1.61i)T
5 1−2.23T 1 - 2.23T
good7 1+(1+i)T+7iT2 1 + (1 + i)T + 7iT^{2}
11 1−4.47iT−11T2 1 - 4.47iT - 11T^{2}
13 1+(3−3i)T−13iT2 1 + (3 - 3i)T - 13iT^{2}
17 1+(−2.23+2.23i)T−17iT2 1 + (-2.23 + 2.23i)T - 17iT^{2}
19 1+2iT−19T2 1 + 2iT - 19T^{2}
23 1+(2.23+2.23i)T+23iT2 1 + (2.23 + 2.23i)T + 23iT^{2}
29 1+4.47T+29T2 1 + 4.47T + 29T^{2}
31 1−4T+31T2 1 - 4T + 31T^{2}
37 1+(3+3i)T+37iT2 1 + (3 + 3i)T + 37iT^{2}
41 1+8.94iT−41T2 1 + 8.94iT - 41T^{2}
43 1+(3−3i)T−43iT2 1 + (3 - 3i)T - 43iT^{2}
47 1+(6.70−6.70i)T−47iT2 1 + (6.70 - 6.70i)T - 47iT^{2}
53 1+(−2.23−2.23i)T+53iT2 1 + (-2.23 - 2.23i)T + 53iT^{2}
59 1−8.94T+59T2 1 - 8.94T + 59T^{2}
61 1+6T+61T2 1 + 6T + 61T^{2}
67 1+(1+i)T+67iT2 1 + (1 + i)T + 67iT^{2}
71 1+4.47iT−71T2 1 + 4.47iT - 71T^{2}
73 1+(−1+i)T−73iT2 1 + (-1 + i)T - 73iT^{2}
79 1+6iT−79T2 1 + 6iT - 79T^{2}
83 1+(−6.70−6.70i)T+83iT2 1 + (-6.70 - 6.70i)T + 83iT^{2}
89 1−4.47T+89T2 1 - 4.47T + 89T^{2}
97 1+(−9−9i)T+97iT2 1 + (-9 - 9i)T + 97iT^{2}
show more
show less
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−14.66432242693590277964814384018, −13.77601355339610360692790454073, −12.77369705294605892431783409484, −11.88790023898679746609720468116, −10.31517972439760862111967515152, −9.299186274524804035335087601220, −7.41727364560654563618102525190, −6.54806518347674944274692276756, −5.00569969556774291250750573922, −2.15777231959226116393597609132, 3.21855912675630881585355836082, 5.33541712393311827841809943575, 6.14693231226485150864417260201, 8.396741378868973744267835407080, 9.684992825696092715715463123807, 10.39772960952919280695046285176, 11.72583818831365035929475099548, 13.04250042223342786131471706537, 14.25961440418616946764541746827, 15.23423930823948324375620100041

Graph of the ZZ-function along the critical line