↑

Properties

Label 2-70-35.4-c1-0-3
Degree 22
Conductor 7070
Sign 0.208+0.978i0.208 + 0.978i
Analytic cond. 0.5589520.558952
Root an. cond. 0.7476310.747631
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.866 − 0.5i)2-s + (−2.59 − 1.5i)3-s + (0.499 − 0.866i)4-s + (1.23 − 1.86i)5-s − 3·6-s + (0.866 + 2.5i)7-s − 0.999i·8-s + (3 + 5.19i)9-s + (0.133 − 2.23i)10-s + (−2.59 + 1.50i)12-s + 2i·13-s + (2 + 1.73i)14-s + (−6 + 3i)15-s + (−0.5 − 0.866i)16-s + (1.73 + i)17-s + (5.19 + 3i)18-s + ⋯
L(s)  = 1  + (0.612 − 0.353i)2-s + (−1.49 − 0.866i)3-s + (0.249 − 0.433i)4-s + (0.550 − 0.834i)5-s − 1.22·6-s + (0.327 + 0.944i)7-s − 0.353i·8-s + (1 + 1.73i)9-s + (0.0423 − 0.705i)10-s + (−0.749 + 0.433i)12-s + 0.554i·13-s + (0.534 + 0.462i)14-s + (−1.54 + 0.774i)15-s + (−0.125 − 0.216i)16-s + (0.420 + 0.242i)17-s + (1.22 + 0.707i)18-s + ⋯

Functional equation

Λ(s)=(70s/2 ΓC(s) L(s)=((0.208+0.978i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 70 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.208 + 0.978i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(70s/2 ΓC(s+1/2) L(s)=((0.208+0.978i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 70 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.208 + 0.978i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 7070    =    2⋅5⋅72 \cdot 5 \cdot 7
Sign: 0.208+0.978i0.208 + 0.978i
Analytic conductor: 0.5589520.558952
Root analytic conductor: 0.7476310.747631
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ70(39,⋅)\chi_{70} (39, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 70, ( :1/2), 0.208+0.978i)(2,\ 70,\ (\ :1/2),\ 0.208 + 0.978i)

Particular Values

L(1)L(1) ≈\approx 0.708696−0.573475i0.708696 - 0.573475i
L(12)L(\frac12) ≈\approx 0.708696−0.573475i0.708696 - 0.573475i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(−0.866+0.5i)T 1 + (-0.866 + 0.5i)T
5 1+(−1.23+1.86i)T 1 + (-1.23 + 1.86i)T
7 1+(−0.866−2.5i)T 1 + (-0.866 - 2.5i)T
good3 1+(2.59+1.5i)T+(1.5+2.59i)T2 1 + (2.59 + 1.5i)T + (1.5 + 2.59i)T^{2}
11 1+(−5.5−9.52i)T2 1 + (-5.5 - 9.52i)T^{2}
13 1−2iT−13T2 1 - 2iT - 13T^{2}
17 1+(−1.73−i)T+(8.5+14.7i)T2 1 + (-1.73 - i)T + (8.5 + 14.7i)T^{2}
19 1+(1+1.73i)T+(−9.5+16.4i)T2 1 + (1 + 1.73i)T + (-9.5 + 16.4i)T^{2}
23 1+(−0.866+0.5i)T+(11.5−19.9i)T2 1 + (-0.866 + 0.5i)T + (11.5 - 19.9i)T^{2}
29 1−T+29T2 1 - T + 29T^{2}
31 1+(5−8.66i)T+(−15.5−26.8i)T2 1 + (5 - 8.66i)T + (-15.5 - 26.8i)T^{2}
37 1+(6.92−4i)T+(18.5−32.0i)T2 1 + (6.92 - 4i)T + (18.5 - 32.0i)T^{2}
41 1+3T+41T2 1 + 3T + 41T^{2}
43 1+5iT−43T2 1 + 5iT - 43T^{2}
47 1+(−6.92+4i)T+(23.5−40.7i)T2 1 + (-6.92 + 4i)T + (23.5 - 40.7i)T^{2}
53 1+(5.19+3i)T+(26.5+45.8i)T2 1 + (5.19 + 3i)T + (26.5 + 45.8i)T^{2}
59 1+(−1+1.73i)T+(−29.5−51.0i)T2 1 + (-1 + 1.73i)T + (-29.5 - 51.0i)T^{2}
61 1+(−4.5−7.79i)T+(−30.5+52.8i)T2 1 + (-4.5 - 7.79i)T + (-30.5 + 52.8i)T^{2}
67 1+(−6.06−3.5i)T+(33.5+58.0i)T2 1 + (-6.06 - 3.5i)T + (33.5 + 58.0i)T^{2}
71 1−6T+71T2 1 - 6T + 71T^{2}
73 1+(8.66+5i)T+(36.5+63.2i)T2 1 + (8.66 + 5i)T + (36.5 + 63.2i)T^{2}
79 1+(5+8.66i)T+(−39.5+68.4i)T2 1 + (5 + 8.66i)T + (-39.5 + 68.4i)T^{2}
83 1−9iT−83T2 1 - 9iT - 83T^{2}
89 1+(3.5+6.06i)T+(−44.5+77.0i)T2 1 + (3.5 + 6.06i)T + (-44.5 + 77.0i)T^{2}
97 1−97T2 1 - 97T^{2}
show more
show less
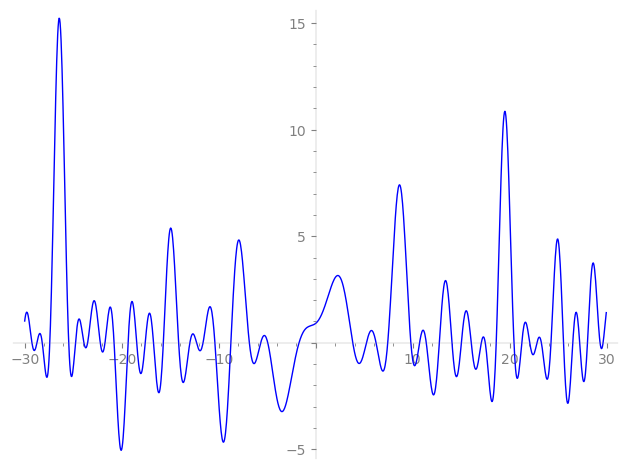
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−14.12965696730763055122141290614, −12.97293312071078694527113425833, −12.28117800541804475435058764838, −11.61538378737480570837057754073, −10.39247182324690179314206702678, −8.745418404231952740762255374242, −6.84056006356308735358610205757, −5.67341944065894258133949738608, −4.94425525517896381904069506670, −1.72010951584794250908056878961, 3.81770243724999369473839296429, 5.22625661068966867787152024155, 6.21924130930249366732776460977, 7.42171420125352958769405301091, 9.806660943830376443911478166377, 10.70567023931131578997706477842, 11.39444897057865450990211041701, 12.74016830980429047250725311396, 14.04688400236946830188324989970, 15.01378994561969518513406450315

Graph of the ZZ-function along the critical line