↑

Properties

Label 2-850-17.13-c1-0-26
Degree 22
Conductor 850850
Sign −0.904−0.426i-0.904 - 0.426i
Analytic cond. 6.787286.78728
Root an. cond. 2.605242.60524
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − i·2-s + (−1.90 − 1.90i)3-s − 4-s + (−1.90 + 1.90i)6-s + (2.69 − 2.69i)7-s + i·8-s + 4.28i·9-s + (3.82 − 3.82i)11-s + (1.90 + 1.90i)12-s − 2.11·13-s + (−2.69 − 2.69i)14-s + 16-s + (−0.908 − 4.02i)17-s + 4.28·18-s − 7.10i·19-s + ⋯
L(s)  = 1  − 0.707i·2-s + (−1.10 − 1.10i)3-s − 0.5·4-s + (−0.779 + 0.779i)6-s + (1.02 − 1.02i)7-s + 0.353i·8-s + 1.42i·9-s + (1.15 − 1.15i)11-s + (0.550 + 0.550i)12-s − 0.586·13-s + (−0.721 − 0.721i)14-s + 0.250·16-s + (−0.220 − 0.975i)17-s + 1.00·18-s − 1.62i·19-s + ⋯

Functional equation

Λ(s)=(850s/2 ΓC(s) L(s)=((−0.904−0.426i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 850 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.904 - 0.426i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(850s/2 ΓC(s+1/2) L(s)=((−0.904−0.426i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 850 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.904 - 0.426i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 850850    =    2⋅52⋅172 \cdot 5^{2} \cdot 17
Sign: −0.904−0.426i-0.904 - 0.426i
Analytic conductor: 6.787286.78728
Root analytic conductor: 2.605242.60524
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ850(251,⋅)\chi_{850} (251, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 850, ( :1/2), −0.904−0.426i)(2,\ 850,\ (\ :1/2),\ -0.904 - 0.426i)

Particular Values

L(1)L(1) ≈\approx 0.222703+0.994178i0.222703 + 0.994178i
L(12)L(\frac12) ≈\approx 0.222703+0.994178i0.222703 + 0.994178i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+iT 1 + iT
5 1 1
17 1+(0.908+4.02i)T 1 + (0.908 + 4.02i)T
good3 1+(1.90+1.90i)T+3iT2 1 + (1.90 + 1.90i)T + 3iT^{2}
7 1+(−2.69+2.69i)T−7iT2 1 + (-2.69 + 2.69i)T - 7iT^{2}
11 1+(−3.82+3.82i)T−11iT2 1 + (-3.82 + 3.82i)T - 11iT^{2}
13 1+2.11T+13T2 1 + 2.11T + 13T^{2}
19 1+7.10iT−19T2 1 + 7.10iT - 19T^{2}
23 1+(−0.585+0.585i)T−23iT2 1 + (-0.585 + 0.585i)T - 23iT^{2}
29 1+(−3.49−3.49i)T+29iT2 1 + (-3.49 - 3.49i)T + 29iT^{2}
31 1+(0.779+0.779i)T+31iT2 1 + (0.779 + 0.779i)T + 31iT^{2}
37 1+(−7.52−7.52i)T+37iT2 1 + (-7.52 - 7.52i)T + 37iT^{2}
41 1+(4.39−4.39i)T−41iT2 1 + (4.39 - 4.39i)T - 41iT^{2}
43 1−7.81iT−43T2 1 - 7.81iT - 43T^{2}
47 1+2.29T+47T2 1 + 2.29T + 47T^{2}
53 1+3.28iT−53T2 1 + 3.28iT - 53T^{2}
59 1+0.555iT−59T2 1 + 0.555iT - 59T^{2}
61 1+(−2.89+2.89i)T−61iT2 1 + (-2.89 + 2.89i)T - 61iT^{2}
67 1−3.97T+67T2 1 - 3.97T + 67T^{2}
71 1+(4.59+4.59i)T+71iT2 1 + (4.59 + 4.59i)T + 71iT^{2}
73 1+(7.45+7.45i)T+73iT2 1 + (7.45 + 7.45i)T + 73iT^{2}
79 1+(9.61−9.61i)T−79iT2 1 + (9.61 - 9.61i)T - 79iT^{2}
83 1−4.04iT−83T2 1 - 4.04iT - 83T^{2}
89 1+11.5T+89T2 1 + 11.5T + 89T^{2}
97 1+(−0.600−0.600i)T+97iT2 1 + (-0.600 - 0.600i)T + 97iT^{2}
show more
show less
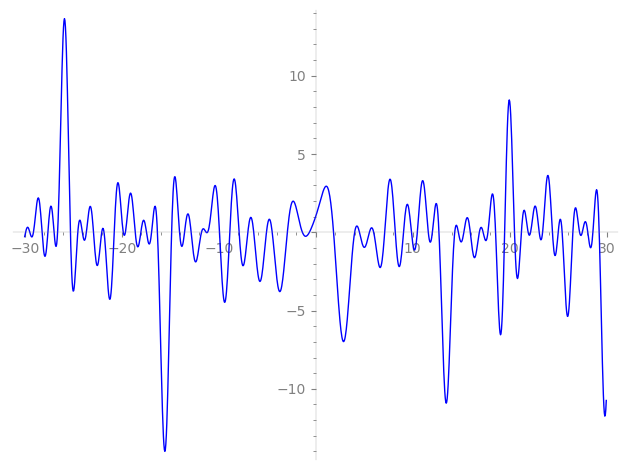
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−9.920293666893193757359941877377, −8.860400436596583012811897533497, −7.897850678906681521414739950837, −6.99585262807052972866382013324, −6.38950873029964362860951459612, −5.07869111605367247375296072039, −4.48581724619899995667787966151, −2.92481290835022831738068855657, −1.37340181775045590364771481408, −0.65309757836195555815646416128, 1.83912353696628495215158021427, 4.01301594205041649020233746286, 4.50831386080924658383799506347, 5.53249250567467896633882862744, 5.97401305183480450728319597127, 7.10627650275090400400137261747, 8.200226014956690316310789830313, 9.047496512101520098293021208522, 9.868083128251760000144692833474, 10.47280411247258515802795753731

Graph of the ZZ-function along the critical line