↑

Properties

Label 2-936-117.31-c0-0-1
Degree $2$
Conductor $936$
Sign $-0.311 + 0.950i$
Analytic cond. $0.467124$
Root an. cond. $0.683465$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.5 − 0.866i)3-s + (−0.366 − 1.36i)5-s + (−0.499 − 0.866i)9-s + (−0.5 + 0.866i)13-s + (−1.36 − 0.366i)15-s − i·17-s + (0.866 + 0.5i)23-s + (−0.866 + 0.5i)25-s − 0.999·27-s + (0.366 + 1.36i)31-s + (−1 − i)37-s + (0.499 + 0.866i)39-s + (−0.366 − 1.36i)41-s + (0.866 − 0.5i)43-s + (−0.999 + 0.999i)45-s + ⋯
L(s)  = 1  + (0.5 − 0.866i)3-s + (−0.366 − 1.36i)5-s + (−0.499 − 0.866i)9-s + (−0.5 + 0.866i)13-s + (−1.36 − 0.366i)15-s − i·17-s + (0.866 + 0.5i)23-s + (−0.866 + 0.5i)25-s − 0.999·27-s + (0.366 + 1.36i)31-s + (−1 − i)37-s + (0.499 + 0.866i)39-s + (−0.366 − 1.36i)41-s + (0.866 − 0.5i)43-s + (−0.999 + 0.999i)45-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 936 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.311 + 0.950i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 936 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.311 + 0.950i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(936\)    =    \(2^{3} \cdot 3^{2} \cdot 13\)
Sign: $-0.311 + 0.950i$
Analytic conductor: \(0.467124\)
Root analytic conductor: \(0.683465\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{936} (265, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 936,\ (\ :0),\ -0.311 + 0.950i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.042169258\)
\(L(\frac12)\) \(\approx\) \(1.042169258\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 \)
3 \( 1 + (-0.5 + 0.866i)T \)
13 \( 1 + (0.5 - 0.866i)T \)
good5 \( 1 + (0.366 + 1.36i)T + (-0.866 + 0.5i)T^{2} \)
7 \( 1 + (-0.866 - 0.5i)T^{2} \)
11 \( 1 + (-0.866 - 0.5i)T^{2} \)
17 \( 1 + iT - T^{2} \)
19 \( 1 - iT^{2} \)
23 \( 1 + (-0.866 - 0.5i)T + (0.5 + 0.866i)T^{2} \)
29 \( 1 + (-0.5 + 0.866i)T^{2} \)
31 \( 1 + (-0.366 - 1.36i)T + (-0.866 + 0.5i)T^{2} \)
37 \( 1 + (1 + i)T + iT^{2} \)
41 \( 1 + (0.366 + 1.36i)T + (-0.866 + 0.5i)T^{2} \)
43 \( 1 + (-0.866 + 0.5i)T + (0.5 - 0.866i)T^{2} \)
47 \( 1 + (0.366 - 1.36i)T + (-0.866 - 0.5i)T^{2} \)
53 \( 1 - T + T^{2} \)
59 \( 1 + (-1.36 + 0.366i)T + (0.866 - 0.5i)T^{2} \)
61 \( 1 + (0.5 + 0.866i)T + (-0.5 + 0.866i)T^{2} \)
67 \( 1 + (-0.866 + 0.5i)T^{2} \)
71 \( 1 - iT^{2} \)
73 \( 1 + (-1 - i)T + iT^{2} \)
79 \( 1 + (-0.5 - 0.866i)T + (-0.5 + 0.866i)T^{2} \)
83 \( 1 + (1.36 + 0.366i)T + (0.866 + 0.5i)T^{2} \)
89 \( 1 + iT^{2} \)
97 \( 1 + (0.866 + 0.5i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

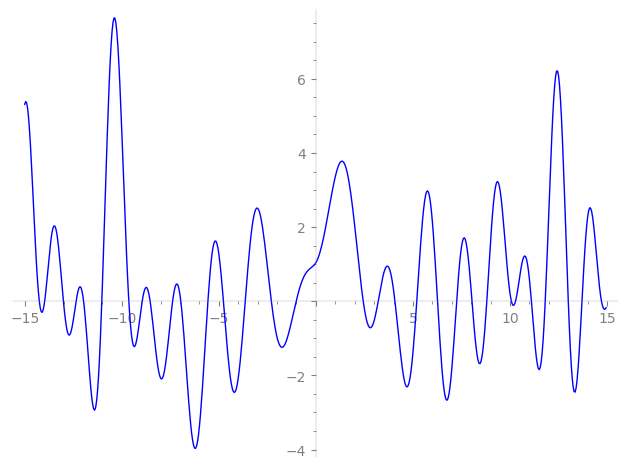
Imaginary part of the first few zeros on the critical line

−9.634889844275284843916662474084, −8.946806901484747744251020316446, −8.538787504262126513338558787988, −7.38009908491076695743494678413, −6.95804925045234238036711657787, −5.56208790554890446908582109494, −4.76371234894154358788424743507, −3.63989589581498703835923650270, −2.29472328275643872310291942626, −1.01568278684770457234785137423, 2.43725793796328625110298629381, 3.20948182947219682025111276881, 4.07174289346193477666585577473, 5.19548002672924797710506199922, 6.26531361749156595718395068163, 7.24985717774897542699329469432, 8.040729084737041350320970556565, 8.802833819231850772555676477298, 10.06901367579963915532553857959, 10.28262601030309020956755927548

Graph of the $Z$-function along the critical line