↑

Properties

Label 4-1280e2-1.1-c1e2-0-10
Degree 44
Conductor 16384001638400
Sign 11
Analytic cond. 104.465104.465
Root an. cond. 3.197003.19700
Motivic weight 11
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 6·9-s − 4·11-s − 12·19-s − 5·25-s − 4·41-s − 6·49-s + 28·59-s + 27·81-s + 28·89-s − 24·99-s − 10·121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s + 6·169-s − 72·171-s + 173-s + 179-s + 181-s + 191-s + 193-s + ⋯
L(s)  = 1  + 2·9-s − 1.20·11-s − 2.75·19-s − 25-s − 0.624·41-s − 6/7·49-s + 3.64·59-s + 3·81-s + 2.96·89-s − 2.41·99-s − 0.909·121-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s + 0.0819·149-s + 0.0813·151-s + 0.0798·157-s + 0.0783·163-s + 0.0773·167-s + 6/13·169-s − 5.50·171-s + 0.0760·173-s + 0.0747·179-s + 0.0743·181-s + 0.0723·191-s + 0.0719·193-s + ⋯

Functional equation

Λ(s)=(1638400s/2 ΓC(s)2 L(s)=( Λ(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 1638400 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}
Λ(s)=(1638400s/2 ΓC(s+1/2)2 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 1638400 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 44
Conductor: 16384001638400    =    216⋅522^{16} \cdot 5^{2}
Sign: 11
Analytic conductor: 104.465104.465
Root analytic conductor: 3.197003.19700
Motivic weight: 11
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (4, 1638400, ( :1/2,1/2), 1)(4,\ 1638400,\ (\ :1/2, 1/2),\ 1)

Particular Values

L(1)L(1) ≈\approx 1.6468476341.646847634
L(12)L(\frac12) ≈\approx 1.6468476341.646847634
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2 1 1
5C2C_2 1+pT2 1 + p T^{2}
good3C2C_2 (1−pT2)2 ( 1 - p T^{2} )^{2}
7C22C_2^2 1+6T2+p2T4 1 + 6 T^{2} + p^{2} T^{4}
11C2C_2 (1+2T+pT2)2 ( 1 + 2 T + p T^{2} )^{2}
13C22C_2^2 1−6T2+p2T4 1 - 6 T^{2} + p^{2} T^{4}
17C2C_2 (1−pT2)2 ( 1 - p T^{2} )^{2}
19C2C_2 (1+6T+pT2)2 ( 1 + 6 T + p T^{2} )^{2}
23C22C_2^2 1−26T2+p2T4 1 - 26 T^{2} + p^{2} T^{4}
29C2C_2 (1+pT2)2 ( 1 + p T^{2} )^{2}
31C2C_2 (1+pT2)2 ( 1 + p T^{2} )^{2}
37C22C_2^2 1−54T2+p2T4 1 - 54 T^{2} + p^{2} T^{4}
41C2C_2 (1+2T+pT2)2 ( 1 + 2 T + p T^{2} )^{2}
43C2C_2 (1−pT2)2 ( 1 - p T^{2} )^{2}
47C22C_2^2 1+86T2+p2T4 1 + 86 T^{2} + p^{2} T^{4}
53C22C_2^2 1+74T2+p2T4 1 + 74 T^{2} + p^{2} T^{4}
59C2C_2 (1−14T+pT2)2 ( 1 - 14 T + p T^{2} )^{2}
61C2C_2 (1+pT2)2 ( 1 + p T^{2} )^{2}
67C2C_2 (1−pT2)2 ( 1 - p T^{2} )^{2}
71C2C_2 (1+pT2)2 ( 1 + p T^{2} )^{2}
73C2C_2 (1−pT2)2 ( 1 - p T^{2} )^{2}
79C2C_2 (1+pT2)2 ( 1 + p T^{2} )^{2}
83C2C_2 (1−pT2)2 ( 1 - p T^{2} )^{2}
89C2C_2 (1−14T+pT2)2 ( 1 - 14 T + p T^{2} )^{2}
97C2C_2 (1−pT2)2 ( 1 - p T^{2} )^{2}
show more
show less
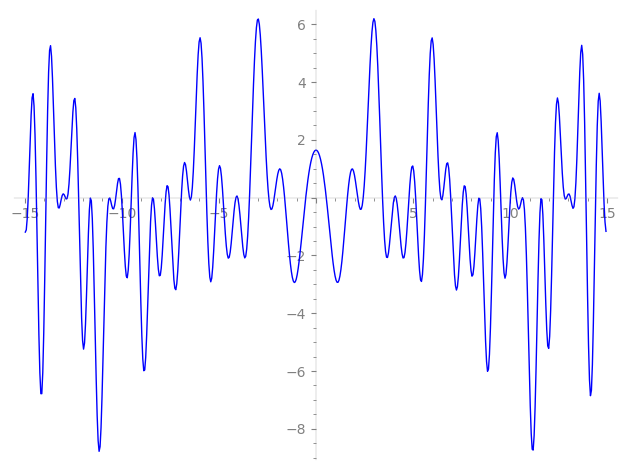
   L(s)=∏p ∏j=14(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.01189834274754399308534160477, −9.508218434809640462552057689155, −9.154939644273593689723852753604, −8.416304929789343801293118197581, −8.389866350791385063712407009806, −7.74592460986006238385529971400, −7.55725113131992085501945558784, −6.93648865182708136909338145864, −6.51323186750480796166338039502, −6.42293634005169415510828363066, −5.64325386138238628445848631646, −5.13170956332301373270710468705, −4.78717868140838772970687718482, −4.12362414051404373152275425894, −4.02991545464335586041913743014, −3.42512443476988478287900229256, −2.43094823568408556388572935045, −2.15052945118002727801548050054, −1.61534907303435197837576917532, −0.52902945122450277243009553487, 0.52902945122450277243009553487, 1.61534907303435197837576917532, 2.15052945118002727801548050054, 2.43094823568408556388572935045, 3.42512443476988478287900229256, 4.02991545464335586041913743014, 4.12362414051404373152275425894, 4.78717868140838772970687718482, 5.13170956332301373270710468705, 5.64325386138238628445848631646, 6.42293634005169415510828363066, 6.51323186750480796166338039502, 6.93648865182708136909338145864, 7.55725113131992085501945558784, 7.74592460986006238385529971400, 8.389866350791385063712407009806, 8.416304929789343801293118197581, 9.154939644273593689723852753604, 9.508218434809640462552057689155, 10.01189834274754399308534160477

Graph of the ZZ-function along the critical line