↑

Properties

Label 4-1280e2-1.1-c1e2-0-41
Degree 44
Conductor 16384001638400
Sign 11
Analytic cond. 104.465104.465
Root an. cond. 3.197003.19700
Motivic weight 11
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 2·3-s + 4·5-s − 6·7-s + 2·9-s + 4·11-s + 6·13-s + 8·15-s + 2·17-s − 12·21-s − 2·23-s + 11·25-s + 6·27-s + 8·33-s − 24·35-s − 2·37-s + 12·39-s + 20·41-s − 10·43-s + 8·45-s + 6·47-s + 18·49-s + 4·51-s + 10·53-s + 16·55-s − 12·63-s + 24·65-s + 2·67-s + ⋯
L(s)  = 1  + 1.15·3-s + 1.78·5-s − 2.26·7-s + 2/3·9-s + 1.20·11-s + 1.66·13-s + 2.06·15-s + 0.485·17-s − 2.61·21-s − 0.417·23-s + 11/5·25-s + 1.15·27-s + 1.39·33-s − 4.05·35-s − 0.328·37-s + 1.92·39-s + 3.12·41-s − 1.52·43-s + 1.19·45-s + 0.875·47-s + 18/7·49-s + 0.560·51-s + 1.37·53-s + 2.15·55-s − 1.51·63-s + 2.97·65-s + 0.244·67-s + ⋯

Functional equation

Λ(s)=(1638400s/2 ΓC(s)2 L(s)=( Λ(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 1638400 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}
Λ(s)=(1638400s/2 ΓC(s+1/2)2 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 1638400 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 44
Conductor: 16384001638400    =    216⋅522^{16} \cdot 5^{2}
Sign: 11
Analytic conductor: 104.465104.465
Root analytic conductor: 3.197003.19700
Motivic weight: 11
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (4, 1638400, ( :1/2,1/2), 1)(4,\ 1638400,\ (\ :1/2, 1/2),\ 1)

Particular Values

L(1)L(1) ≈\approx 4.9738851774.973885177
L(12)L(\frac12) ≈\approx 4.9738851774.973885177
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2 1 1
5C2C_2 1−4T+pT2 1 - 4 T + p T^{2}
good3C22C_2^2 1−2T+2T2−2pT3+p2T4 1 - 2 T + 2 T^{2} - 2 p T^{3} + p^{2} T^{4}
7C22C_2^2 1+6T+18T2+6pT3+p2T4 1 + 6 T + 18 T^{2} + 6 p T^{3} + p^{2} T^{4}
11C2C_2 (1−2T+pT2)2 ( 1 - 2 T + p T^{2} )^{2}
13C22C_2^2 1−6T+18T2−6pT3+p2T4 1 - 6 T + 18 T^{2} - 6 p T^{3} + p^{2} T^{4}
17C22C_2^2 1−2T+2T2−2pT3+p2T4 1 - 2 T + 2 T^{2} - 2 p T^{3} + p^{2} T^{4}
19C22C_2^2 1−22T2+p2T4 1 - 22 T^{2} + p^{2} T^{4}
23C22C_2^2 1+2T+2T2+2pT3+p2T4 1 + 2 T + 2 T^{2} + 2 p T^{3} + p^{2} T^{4}
29C2C_2 (1+pT2)2 ( 1 + p T^{2} )^{2}
31C22C_2^2 1+38T2+p2T4 1 + 38 T^{2} + p^{2} T^{4}
37C22C_2^2 1+2T+2T2+2pT3+p2T4 1 + 2 T + 2 T^{2} + 2 p T^{3} + p^{2} T^{4}
41C2C_2 (1−10T+pT2)2 ( 1 - 10 T + p T^{2} )^{2}
43C22C_2^2 1+10T+50T2+10pT3+p2T4 1 + 10 T + 50 T^{2} + 10 p T^{3} + p^{2} T^{4}
47C22C_2^2 1−6T+18T2−6pT3+p2T4 1 - 6 T + 18 T^{2} - 6 p T^{3} + p^{2} T^{4}
53C2C_2 (1−14T+pT2)(1+4T+pT2) ( 1 - 14 T + p T^{2} )( 1 + 4 T + p T^{2} )
59C22C_2^2 1+26T2+p2T4 1 + 26 T^{2} + p^{2} T^{4}
61C22C_2^2 1−118T2+p2T4 1 - 118 T^{2} + p^{2} T^{4}
67C22C_2^2 1−2T+2T2−2pT3+p2T4 1 - 2 T + 2 T^{2} - 2 p T^{3} + p^{2} T^{4}
71C22C_2^2 1−138T2+p2T4 1 - 138 T^{2} + p^{2} T^{4}
73C22C_2^2 1+2T+2T2+2pT3+p2T4 1 + 2 T + 2 T^{2} + 2 p T^{3} + p^{2} T^{4}
79C2C_2 (1+8T+pT2)2 ( 1 + 8 T + p T^{2} )^{2}
83C22C_2^2 1−10T+50T2−10pT3+p2T4 1 - 10 T + 50 T^{2} - 10 p T^{3} + p^{2} T^{4}
89C2C_2 (1−10T+pT2)(1+10T+pT2) ( 1 - 10 T + p T^{2} )( 1 + 10 T + p T^{2} )
97C22C_2^2 1+6T+18T2+6pT3+p2T4 1 + 6 T + 18 T^{2} + 6 p T^{3} + p^{2} T^{4}
show more
show less
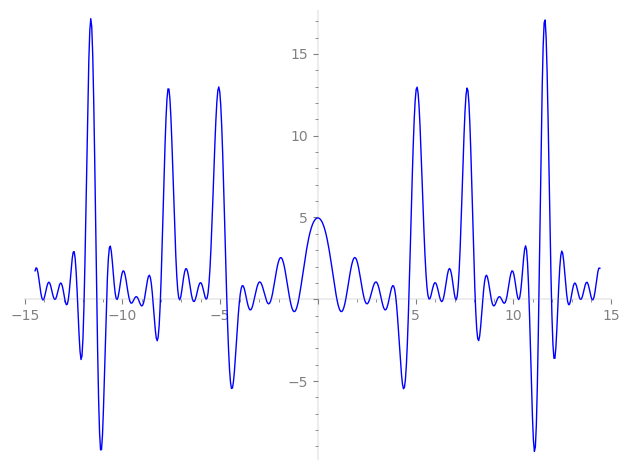
   L(s)=∏p ∏j=14(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−9.645350837740558908925893226743, −9.402456803584422082986961650440, −9.183588706578470632279672495318, −8.875916381237804046764419913818, −8.442967585645943387558307781780, −8.054915792416821113508114592346, −7.09784449636194623806615124941, −7.04691145765800249607407565859, −6.41447180530827700891439005324, −6.26544967810012028475264976236, −5.71220766864053706978570655988, −5.70035539540159393762998946890, −4.65789450072451515343506568620, −4.00085779896879103884871738354, −3.64492132258854567330998707155, −3.25428908236209704701738066116, −2.65187037517861713573738993739, −2.38533361247367005137780260175, −1.42990253219613563328555726280, −0.976448526410779716129716993104, 0.976448526410779716129716993104, 1.42990253219613563328555726280, 2.38533361247367005137780260175, 2.65187037517861713573738993739, 3.25428908236209704701738066116, 3.64492132258854567330998707155, 4.00085779896879103884871738354, 4.65789450072451515343506568620, 5.70035539540159393762998946890, 5.71220766864053706978570655988, 6.26544967810012028475264976236, 6.41447180530827700891439005324, 7.04691145765800249607407565859, 7.09784449636194623806615124941, 8.054915792416821113508114592346, 8.442967585645943387558307781780, 8.875916381237804046764419913818, 9.183588706578470632279672495318, 9.402456803584422082986961650440, 9.645350837740558908925893226743

Graph of the ZZ-function along the critical line