↑

Properties

Label 4-345600-1.1-c1e2-0-0
Degree 44
Conductor 345600345600
Sign 11
Analytic cond. 22.035722.0357
Root an. cond. 2.166612.16661
Motivic weight 11
Arithmetic yes
Rational yes
Primitive yes
Self-dual yes
Analytic rank 00

Origins

Downloads

Learn more

Normalization:  

Dirichlet series

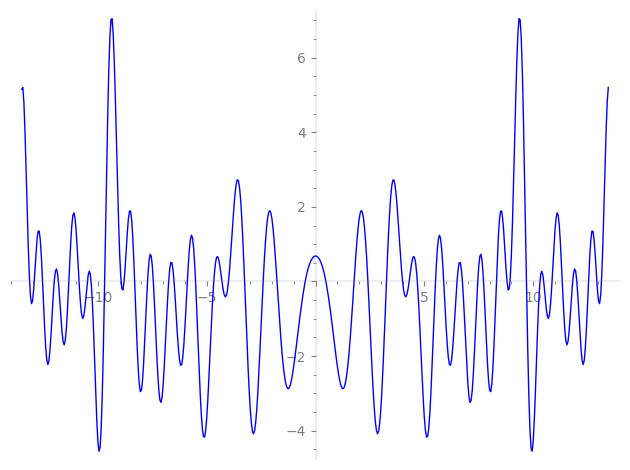
L(s)  = 1  − 3-s − 2·5-s + 9-s + 2·15-s − 12·19-s − 25-s − 27-s − 4·43-s − 2·45-s + 8·47-s + 10·49-s − 4·53-s + 12·57-s + 4·67-s − 12·71-s − 8·73-s + 75-s + 81-s + 24·95-s + 12·97-s + 12·101-s − 10·121-s + 12·125-s + 127-s + 4·129-s + 131-s + 2·135-s + ⋯
L(s)  = 1  − 0.577·3-s − 0.894·5-s + 1/3·9-s + 0.516·15-s − 2.75·19-s − 1/5·25-s − 0.192·27-s − 0.609·43-s − 0.298·45-s + 1.16·47-s + 10/7·49-s − 0.549·53-s + 1.58·57-s + 0.488·67-s − 1.42·71-s − 0.936·73-s + 0.115·75-s + 1/9·81-s + 2.46·95-s + 1.21·97-s + 1.19·101-s − 0.909·121-s + 1.07·125-s + 0.0887·127-s + 0.352·129-s + 0.0873·131-s + 0.172·135-s + ⋯

Functional equation

Λ(s)=(345600s/2 ΓC(s)2 L(s)=( Λ(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 345600 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}
Λ(s)=(345600s/2 ΓC(s+1/2)2 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 345600 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 44
Conductor: 345600345600    =    29⋅33⋅522^{9} \cdot 3^{3} \cdot 5^{2}
Sign: 11
Analytic conductor: 22.035722.0357
Root analytic conductor: 2.166612.16661
Motivic weight: 11
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: yes
Self-dual: yes
Analytic rank: 00
Selberg data: (4, 345600, ( :1/2,1/2), 1)(4,\ 345600,\ (\ :1/2, 1/2),\ 1)

Particular Values

L(1)L(1) ≈\approx 0.68319642530.6831964253
L(12)L(\frac12) ≈\approx 0.68319642530.6831964253
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2 1 1
3C1C_1 1+T 1 + T
5C2C_2 1+2T+pT2 1 + 2 T + p T^{2}
good7C22C_2^2 1−10T2+p2T4 1 - 10 T^{2} + p^{2} T^{4}
11C22C_2^2 1+10T2+p2T4 1 + 10 T^{2} + p^{2} T^{4}
13C22C_2^2 1+18T2+p2T4 1 + 18 T^{2} + p^{2} T^{4}
17C22C_2^2 1−10T2+p2T4 1 - 10 T^{2} + p^{2} T^{4}
19C2C_2×\timesC2C_2 (1+4T+pT2)(1+8T+pT2) ( 1 + 4 T + p T^{2} )( 1 + 8 T + p T^{2} )
23C2C_2 (1−4T+pT2)(1+4T+pT2) ( 1 - 4 T + p T^{2} )( 1 + 4 T + p T^{2} )
29C2C_2 (1−2T+pT2)(1+2T+pT2) ( 1 - 2 T + p T^{2} )( 1 + 2 T + p T^{2} )
31C22C_2^2 1+38T2+p2T4 1 + 38 T^{2} + p^{2} T^{4}
37C22C_2^2 1−38T2+p2T4 1 - 38 T^{2} + p^{2} T^{4}
41C22C_2^2 1−26T2+p2T4 1 - 26 T^{2} + p^{2} T^{4}
43C2C_2×\timesC2C_2 (1+pT2)(1+4T+pT2) ( 1 + p T^{2} )( 1 + 4 T + p T^{2} )
47C2C_2×\timesC2C_2 (1−8T+pT2)(1+pT2) ( 1 - 8 T + p T^{2} )( 1 + p T^{2} )
53C2C_2×\timesC2C_2 (1−6T+pT2)(1+10T+pT2) ( 1 - 6 T + p T^{2} )( 1 + 10 T + p T^{2} )
59C22C_2^2 1+2T2+p2T4 1 + 2 T^{2} + p^{2} T^{4}
61C22C_2^2 1−58T2+p2T4 1 - 58 T^{2} + p^{2} T^{4}
67C2C_2×\timesC2C_2 (1−12T+pT2)(1+8T+pT2) ( 1 - 12 T + p T^{2} )( 1 + 8 T + p T^{2} )
71C2C_2×\timesC2C_2 (1+pT2)(1+12T+pT2) ( 1 + p T^{2} )( 1 + 12 T + p T^{2} )
73C2C_2×\timesC2C_2 (1+2T+pT2)(1+6T+pT2) ( 1 + 2 T + p T^{2} )( 1 + 6 T + p T^{2} )
79C22C_2^2 1−90T2+p2T4 1 - 90 T^{2} + p^{2} T^{4}
83C2C_2 (1−16T+pT2)(1+16T+pT2) ( 1 - 16 T + p T^{2} )( 1 + 16 T + p T^{2} )
89C22C_2^2 1−90T2+p2T4 1 - 90 T^{2} + p^{2} T^{4}
97C2C_2×\timesC2C_2 (1−10T+pT2)(1−2T+pT2) ( 1 - 10 T + p T^{2} )( 1 - 2 T + p T^{2} )
show more
show less
   L(s)=∏p ∏j=14(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−8.796523279169400324099811274199, −8.311117487892413678982025088035, −7.71916516278321719237455267489, −7.45291882652318289749379821721, −6.74822994356548814377277210941, −6.50122389996814390419899237868, −5.88978115346659328854413481568, −5.51271162729538474767227340615, −4.67629508369109499467730348616, −4.30042216411982689284177737617, −3.99884352876894801076363929522, −3.25909981327213640380196307522, −2.40621497002503574889419611187, −1.77015580864553681627788006708, −0.47534095433036505976960674830, 0.47534095433036505976960674830, 1.77015580864553681627788006708, 2.40621497002503574889419611187, 3.25909981327213640380196307522, 3.99884352876894801076363929522, 4.30042216411982689284177737617, 4.67629508369109499467730348616, 5.51271162729538474767227340615, 5.88978115346659328854413481568, 6.50122389996814390419899237868, 6.74822994356548814377277210941, 7.45291882652318289749379821721, 7.71916516278321719237455267489, 8.311117487892413678982025088035, 8.796523279169400324099811274199

Graph of the ZZ-function along the critical line