↑

Properties

Label 4-800e2-1.1-c1e2-0-23
Degree 44
Conductor 640000640000
Sign 11
Analytic cond. 40.806940.8069
Root an. cond. 2.527452.52745
Motivic weight 11
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 5·9-s + 10·11-s − 10·19-s − 8·29-s + 20·31-s + 10·41-s + 10·49-s − 20·61-s − 20·79-s + 16·81-s + 18·89-s + 50·99-s + 4·101-s − 20·109-s + 53·121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 157-s + 163-s + 167-s + 26·169-s − 50·171-s + 173-s + ⋯
L(s)  = 1  + 5/3·9-s + 3.01·11-s − 2.29·19-s − 1.48·29-s + 3.59·31-s + 1.56·41-s + 10/7·49-s − 2.56·61-s − 2.25·79-s + 16/9·81-s + 1.90·89-s + 5.02·99-s + 0.398·101-s − 1.91·109-s + 4.81·121-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s + 0.0819·149-s + 0.0813·151-s + 0.0798·157-s + 0.0783·163-s + 0.0773·167-s + 2·169-s − 3.82·171-s + 0.0760·173-s + ⋯

Functional equation

Λ(s)=(640000s/2 ΓC(s)2 L(s)=( Λ(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 640000 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(2-s) \end{aligned}
Λ(s)=(640000s/2 ΓC(s+1/2)2 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 640000 ^{s/2} \, \Gamma_{\C}(s+1/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 44
Conductor: 640000640000    =    210⋅542^{10} \cdot 5^{4}
Sign: 11
Analytic conductor: 40.806940.8069
Root analytic conductor: 2.527452.52745
Motivic weight: 11
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (4, 640000, ( :1/2,1/2), 1)(4,\ 640000,\ (\ :1/2, 1/2),\ 1)

Particular Values

L(1)L(1) ≈\approx 2.9294332932.929433293
L(12)L(\frac12) ≈\approx 2.9294332932.929433293
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2 1 1
5 1 1
good3C22C_2^2 1−5T2+p2T4 1 - 5 T^{2} + p^{2} T^{4}
7C22C_2^2 1−10T2+p2T4 1 - 10 T^{2} + p^{2} T^{4}
11C2C_2 (1−5T+pT2)2 ( 1 - 5 T + p T^{2} )^{2}
13C2C_2 (1−pT2)2 ( 1 - p T^{2} )^{2}
17C22C_2^2 1−9T2+p2T4 1 - 9 T^{2} + p^{2} T^{4}
19C2C_2 (1+5T+pT2)2 ( 1 + 5 T + p T^{2} )^{2}
23C22C_2^2 1−10T2+p2T4 1 - 10 T^{2} + p^{2} T^{4}
29C2C_2 (1+4T+pT2)2 ( 1 + 4 T + p T^{2} )^{2}
31C2C_2 (1−10T+pT2)2 ( 1 - 10 T + p T^{2} )^{2}
37C22C_2^2 1+26T2+p2T4 1 + 26 T^{2} + p^{2} T^{4}
41C2C_2 (1−5T+pT2)2 ( 1 - 5 T + p T^{2} )^{2}
43C22C_2^2 1−70T2+p2T4 1 - 70 T^{2} + p^{2} T^{4}
47C22C_2^2 1−30T2+p2T4 1 - 30 T^{2} + p^{2} T^{4}
53C22C_2^2 1−6T2+p2T4 1 - 6 T^{2} + p^{2} T^{4}
59C2C_2 (1+pT2)2 ( 1 + p T^{2} )^{2}
61C2C_2 (1+10T+pT2)2 ( 1 + 10 T + p T^{2} )^{2}
67C22C_2^2 1−125T2+p2T4 1 - 125 T^{2} + p^{2} T^{4}
71C2C_2 (1+pT2)2 ( 1 + p T^{2} )^{2}
73C22C_2^2 1−121T2+p2T4 1 - 121 T^{2} + p^{2} T^{4}
79C2C_2 (1+10T+pT2)2 ( 1 + 10 T + p T^{2} )^{2}
83C22C_2^2 1−165T2+p2T4 1 - 165 T^{2} + p^{2} T^{4}
89C2C_2 (1−9T+pT2)2 ( 1 - 9 T + p T^{2} )^{2}
97C22C_2^2 1−94T2+p2T4 1 - 94 T^{2} + p^{2} T^{4}
show more
show less
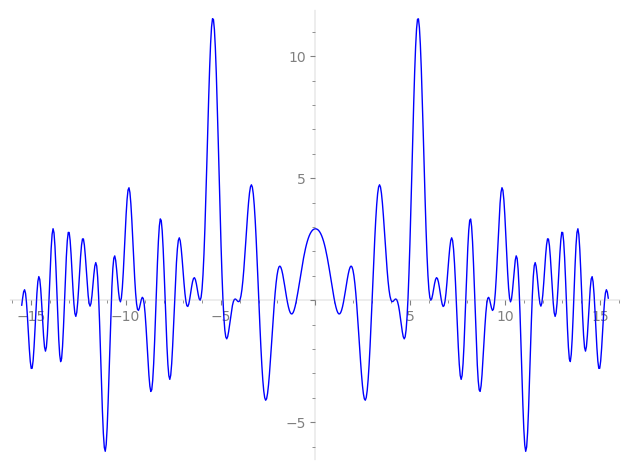
   L(s)=∏p ∏j=14(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.31594868252216130527303204859, −10.24336329187136859823214909874, −9.443304060276063669156847471370, −9.182548237925223439875852383764, −9.052098412177689760219785597876, −8.395686243995346614595435488222, −7.917915564621921843013241512362, −7.41768024801698534526072636162, −6.83354096546273523050079644362, −6.63334225494251240614532572974, −6.08985683562610586151168257123, −6.07247840142845037611962991193, −4.87155616406333745522381581413, −4.29626325416612560031948243571, −4.14482125373430879833007252499, −3.98217840737894371696952159617, −2.98432329207846436430120275537, −2.15556571619399730829542466434, −1.49578044929089267131549979154, −1.00077759881575154699337302663, 1.00077759881575154699337302663, 1.49578044929089267131549979154, 2.15556571619399730829542466434, 2.98432329207846436430120275537, 3.98217840737894371696952159617, 4.14482125373430879833007252499, 4.29626325416612560031948243571, 4.87155616406333745522381581413, 6.07247840142845037611962991193, 6.08985683562610586151168257123, 6.63334225494251240614532572974, 6.83354096546273523050079644362, 7.41768024801698534526072636162, 7.917915564621921843013241512362, 8.395686243995346614595435488222, 9.052098412177689760219785597876, 9.182548237925223439875852383764, 9.443304060276063669156847471370, 10.24336329187136859823214909874, 10.31594868252216130527303204859

Graph of the ZZ-function along the critical line