Dirichlet series
| L(s) = 1 | + 64·2-s + 324·3-s + 2.56e3·4-s + 88·5-s + 2.07e4·6-s + 8.19e4·8-s + 6.56e4·9-s + 5.63e3·10-s + 4.21e4·11-s + 8.29e5·12-s + 5.25e4·13-s + 2.85e4·15-s + 2.29e6·16-s + 2.28e5·17-s + 4.19e6·18-s + 2.05e5·19-s + 2.25e5·20-s + 2.70e6·22-s + 1.84e5·23-s + 2.65e7·24-s − 2.18e6·25-s + 3.36e6·26-s + 1.06e7·27-s + 6.65e6·29-s + 1.82e6·30-s − 8.02e5·31-s + 5.87e7·32-s + ⋯ |
| L(s) = 1 | + 2.82·2-s + 2.30·3-s + 5·4-s + 0.0629·5-s + 6.53·6-s + 7.07·8-s + 10/3·9-s + 0.178·10-s + 0.868·11-s + 11.5·12-s + 0.510·13-s + 0.145·15-s + 35/4·16-s + 0.664·17-s + 9.42·18-s + 0.361·19-s + 0.314·20-s + 2.45·22-s + 0.137·23-s + 16.3·24-s − 1.11·25-s + 1.44·26-s + 3.84·27-s + 1.74·29-s + 0.411·30-s − 0.156·31-s + 9.89·32-s + ⋯ |
Functional equation
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{4} \cdot 7^{8}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(10-s)\end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{4} \cdot 3^{4} \cdot 7^{8}\right)^{s/2} \, \Gamma_{\C}(s+9/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}\]
Invariants
| Degree: | \(8\) |
| Conductor: | \(2^{4} \cdot 3^{4} \cdot 7^{8}\) |
| Sign: | $1$ |
| Analytic conductor: | \(5.25701\times 10^{8}\) |
| Root analytic conductor: | \(12.3053\) |
| Motivic weight: | \(9\) |
| Rational: | yes |
| Arithmetic: | yes |
| Character: | Trivial |
| Primitive: | no |
| Self-dual: | yes |
| Analytic rank: | \(0\) |
| Selberg data: | \((8,\ 2^{4} \cdot 3^{4} \cdot 7^{8} ,\ ( \ : 9/2, 9/2, 9/2, 9/2 ),\ 1 )\) |
Particular Values
| \(L(5)\) | \(\approx\) | \(507.2636408\) |
| \(L(\frac12)\) | \(\approx\) | \(507.2636408\) |
| \(L(\frac{11}{2})\) | not available | |
| \(L(1)\) | not available |
Euler product
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $\Gal(F_p)$ | $F_p(T)$ | |
|---|---|---|---|
| bad | 2 | $C_1$ | \( ( 1 - p^{4} T )^{4} \) |
| 3 | $C_1$ | \( ( 1 - p^{4} T )^{4} \) | |
| 7 | \( 1 \) | ||
| good | 5 | $C_2 \wr S_4$ | \( 1 - 88 T + 2193651 T^{2} + 15386124 p^{3} T^{3} + 195424108984 p^{2} T^{4} + 15386124 p^{12} T^{5} + 2193651 p^{18} T^{6} - 88 p^{27} T^{7} + p^{36} T^{8} \) |
| 11 | $C_2 \wr S_4$ | \( 1 - 42190 T + 3046779249 T^{2} - 226567259465370 T^{3} + 9929645667110327656 T^{4} - 226567259465370 p^{9} T^{5} + 3046779249 p^{18} T^{6} - 42190 p^{27} T^{7} + p^{36} T^{8} \) | |
| 13 | $C_2 \wr S_4$ | \( 1 - 52586 T + 7353996437 T^{2} - 650590694730474 T^{3} - 76125770069193779056 T^{4} - 650590694730474 p^{9} T^{5} + 7353996437 p^{18} T^{6} - 52586 p^{27} T^{7} + p^{36} T^{8} \) | |
| 17 | $C_2 \wr S_4$ | \( 1 - 228860 T + 278671046052 T^{2} - 49970150445514548 T^{3} + \)\(39\!\cdots\!82\)\( T^{4} - 49970150445514548 p^{9} T^{5} + 278671046052 p^{18} T^{6} - 228860 p^{27} T^{7} + p^{36} T^{8} \) | |
| 19 | $C_2 \wr S_4$ | \( 1 - 205294 T + 927092798821 T^{2} - 143725360734961162 T^{3} + \)\(41\!\cdots\!20\)\( T^{4} - 143725360734961162 p^{9} T^{5} + 927092798821 p^{18} T^{6} - 205294 p^{27} T^{7} + p^{36} T^{8} \) | |
| 23 | $C_2 \wr S_4$ | \( 1 - 184060 T + 5755764671196 T^{2} - 471086641801709292 T^{3} + \)\(14\!\cdots\!50\)\( T^{4} - 471086641801709292 p^{9} T^{5} + 5755764671196 p^{18} T^{6} - 184060 p^{27} T^{7} + p^{36} T^{8} \) | |
| 29 | $C_2 \wr S_4$ | \( 1 - 6655460 T + 44931713744991 T^{2} - \)\(19\!\cdots\!20\)\( T^{3} + \)\(88\!\cdots\!36\)\( T^{4} - \)\(19\!\cdots\!20\)\( p^{9} T^{5} + 44931713744991 p^{18} T^{6} - 6655460 p^{27} T^{7} + p^{36} T^{8} \) | |
| 31 | $C_2 \wr S_4$ | \( 1 + 802378 T - 3054104118688 T^{2} + 36173940244272897624 T^{3} + \)\(39\!\cdots\!25\)\( T^{4} + 36173940244272897624 p^{9} T^{5} - 3054104118688 p^{18} T^{6} + 802378 p^{27} T^{7} + p^{36} T^{8} \) | |
| 37 | $C_2 \wr S_4$ | \( 1 + 3681622 T + 119556972955261 T^{2} - \)\(60\!\cdots\!54\)\( T^{3} - \)\(25\!\cdots\!04\)\( T^{4} - \)\(60\!\cdots\!54\)\( p^{9} T^{5} + 119556972955261 p^{18} T^{6} + 3681622 p^{27} T^{7} + p^{36} T^{8} \) | |
| 41 | $C_2 \wr S_4$ | \( 1 - 21746604 T + 1186786818878504 T^{2} - \)\(16\!\cdots\!92\)\( T^{3} + \)\(53\!\cdots\!46\)\( T^{4} - \)\(16\!\cdots\!92\)\( p^{9} T^{5} + 1186786818878504 p^{18} T^{6} - 21746604 p^{27} T^{7} + p^{36} T^{8} \) | |
| 43 | $C_2 \wr S_4$ | \( 1 - 29340146 T + 832121839762849 T^{2} - \)\(34\!\cdots\!02\)\( T^{3} + \)\(42\!\cdots\!96\)\( T^{4} - \)\(34\!\cdots\!02\)\( p^{9} T^{5} + 832121839762849 p^{18} T^{6} - 29340146 p^{27} T^{7} + p^{36} T^{8} \) | |
| 47 | $C_2 \wr S_4$ | \( 1 - 55694460 T + 4982664211181132 T^{2} - \)\(17\!\cdots\!52\)\( T^{3} + \)\(85\!\cdots\!22\)\( T^{4} - \)\(17\!\cdots\!52\)\( p^{9} T^{5} + 4982664211181132 p^{18} T^{6} - 55694460 p^{27} T^{7} + p^{36} T^{8} \) | |
| 53 | $C_2 \wr S_4$ | \( 1 + 92597676 T + 13858937600281223 T^{2} + \)\(85\!\cdots\!60\)\( T^{3} + \)\(69\!\cdots\!36\)\( T^{4} + \)\(85\!\cdots\!60\)\( p^{9} T^{5} + 13858937600281223 p^{18} T^{6} + 92597676 p^{27} T^{7} + p^{36} T^{8} \) | |
| 59 | $C_2 \wr S_4$ | \( 1 + 125014946 T + 31884512686538997 T^{2} + \)\(28\!\cdots\!58\)\( T^{3} + \)\(40\!\cdots\!60\)\( T^{4} + \)\(28\!\cdots\!58\)\( p^{9} T^{5} + 31884512686538997 p^{18} T^{6} + 125014946 p^{27} T^{7} + p^{36} T^{8} \) | |
| 61 | $C_2 \wr S_4$ | \( 1 - 225715700 T + 23178682814505668 T^{2} + \)\(44\!\cdots\!28\)\( T^{3} - \)\(21\!\cdots\!94\)\( T^{4} + \)\(44\!\cdots\!28\)\( p^{9} T^{5} + 23178682814505668 p^{18} T^{6} - 225715700 p^{27} T^{7} + p^{36} T^{8} \) | |
| 67 | $C_2 \wr S_4$ | \( 1 + 78966102 T + 31452864298510481 T^{2} + \)\(23\!\cdots\!02\)\( T^{3} + \)\(10\!\cdots\!64\)\( T^{4} + \)\(23\!\cdots\!02\)\( p^{9} T^{5} + 31452864298510481 p^{18} T^{6} + 78966102 p^{27} T^{7} + p^{36} T^{8} \) | |
| 71 | $C_2 \wr S_4$ | \( 1 - 593356924 T + 298248152852143644 T^{2} - \)\(90\!\cdots\!56\)\( T^{3} + \)\(23\!\cdots\!50\)\( T^{4} - \)\(90\!\cdots\!56\)\( p^{9} T^{5} + 298248152852143644 p^{18} T^{6} - 593356924 p^{27} T^{7} + p^{36} T^{8} \) | |
| 73 | $C_2 \wr S_4$ | \( 1 + 77243046 T + 140353838980856297 T^{2} + \)\(80\!\cdots\!94\)\( T^{3} + \)\(10\!\cdots\!84\)\( T^{4} + \)\(80\!\cdots\!94\)\( p^{9} T^{5} + 140353838980856297 p^{18} T^{6} + 77243046 p^{27} T^{7} + p^{36} T^{8} \) | |
| 79 | $C_2 \wr S_4$ | \( 1 - 1606897150 T + 1269099511878766832 T^{2} - \)\(65\!\cdots\!24\)\( T^{3} + \)\(25\!\cdots\!81\)\( T^{4} - \)\(65\!\cdots\!24\)\( p^{9} T^{5} + 1269099511878766832 p^{18} T^{6} - 1606897150 p^{27} T^{7} + p^{36} T^{8} \) | |
| 83 | $C_2 \wr S_4$ | \( 1 + 139772254 T + 283185185716920849 T^{2} - \)\(18\!\cdots\!62\)\( T^{3} + \)\(59\!\cdots\!76\)\( T^{4} - \)\(18\!\cdots\!62\)\( p^{9} T^{5} + 283185185716920849 p^{18} T^{6} + 139772254 p^{27} T^{7} + p^{36} T^{8} \) | |
| 89 | $C_2 \wr S_4$ | \( 1 + 486711072 T - 24973519342723456 T^{2} + \)\(18\!\cdots\!48\)\( T^{3} + \)\(20\!\cdots\!70\)\( T^{4} + \)\(18\!\cdots\!48\)\( p^{9} T^{5} - 24973519342723456 p^{18} T^{6} + 486711072 p^{27} T^{7} + p^{36} T^{8} \) | |
| 97 | $C_2 \wr S_4$ | \( 1 + 340104618 T + 2099709298554288137 T^{2} + \)\(87\!\cdots\!10\)\( T^{3} + \)\(21\!\cdots\!16\)\( T^{4} + \)\(87\!\cdots\!10\)\( p^{9} T^{5} + 2099709298554288137 p^{18} T^{6} + 340104618 p^{27} T^{7} + p^{36} T^{8} \) | |
| show more | |||
| show less | |||
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
Imaginary part of the first few zeros on the critical line
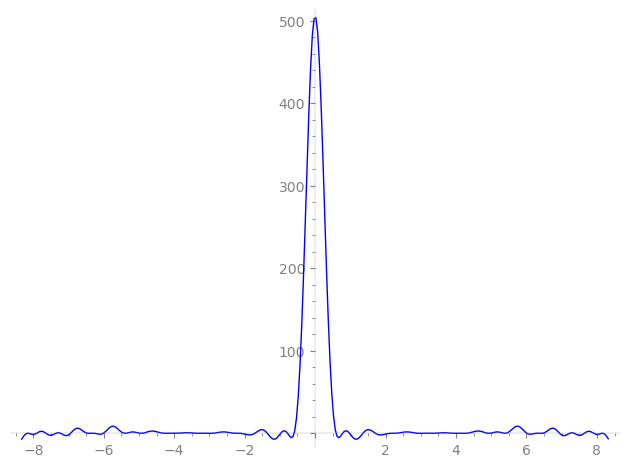
−6.94017425360566360281402984528, −6.45190351868408098903623900790, −6.35604245494728757787542705816, −6.27763127985860891538623945155, −6.01213231260268306673634652770, −5.39303196153791060911023122992, −5.38957014199283157363984513816, −4.95686461251636822980101094130, −4.91091390169688629060511202168, −4.28189692185758705110792317868, −4.16304439258929015694739961445, −4.00752904129962956626172186622, −3.93135120247729492356233948548, −3.36129166924869027404852136686, −3.29240088098575148095304837669, −3.05748869378049314516776822943, −2.90921858971722206182053117578, −2.22794409189828988586016398035, −2.22079947640988946590265192504, −2.19431627710829711346251485378, −1.71163840433361924593654158467, −1.35714310660037321552276362481, −0.977324884859979393526305751610, −0.78088814314790466051835443501, −0.59358615937891549903064233879, 0.59358615937891549903064233879, 0.78088814314790466051835443501, 0.977324884859979393526305751610, 1.35714310660037321552276362481, 1.71163840433361924593654158467, 2.19431627710829711346251485378, 2.22079947640988946590265192504, 2.22794409189828988586016398035, 2.90921858971722206182053117578, 3.05748869378049314516776822943, 3.29240088098575148095304837669, 3.36129166924869027404852136686, 3.93135120247729492356233948548, 4.00752904129962956626172186622, 4.16304439258929015694739961445, 4.28189692185758705110792317868, 4.91091390169688629060511202168, 4.95686461251636822980101094130, 5.38957014199283157363984513816, 5.39303196153791060911023122992, 6.01213231260268306673634652770, 6.27763127985860891538623945155, 6.35604245494728757787542705816, 6.45190351868408098903623900790, 6.94017425360566360281402984528