↑

Properties

Label 2-1110-37.36-c1-0-27
Degree 22
Conductor 11101110
Sign 0.444+0.895i0.444 + 0.895i
Analytic cond. 8.863398.86339
Root an. cond. 2.977142.97714
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

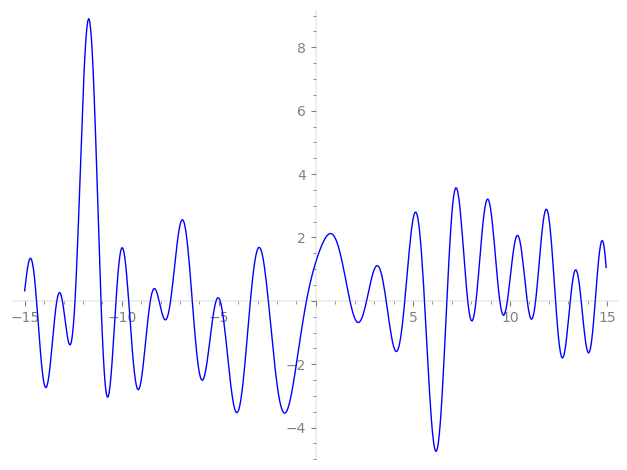
L(s)  = 1  + i·2-s + 3-s − 4-s − i·5-s + i·6-s + 0.374·7-s − i·8-s + 9-s + 10-s − 6.11·11-s − 12-s − 5.44i·13-s + 0.374i·14-s − i·15-s + 16-s − 2.37i·17-s + ⋯
L(s)  = 1  + 0.707i·2-s + 0.577·3-s − 0.5·4-s − 0.447i·5-s + 0.408i·6-s + 0.141·7-s − 0.353i·8-s + 0.333·9-s + 0.316·10-s − 1.84·11-s − 0.288·12-s − 1.51i·13-s + 0.0999i·14-s − 0.258i·15-s + 0.250·16-s − 0.575i·17-s + ⋯

Functional equation

Λ(s)=(1110s/2 ΓC(s) L(s)=((0.444+0.895i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 1110 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.444 + 0.895i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(1110s/2 ΓC(s+1/2) L(s)=((0.444+0.895i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 1110 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.444 + 0.895i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 11101110    =    2⋅3⋅5⋅372 \cdot 3 \cdot 5 \cdot 37
Sign: 0.444+0.895i0.444 + 0.895i
Analytic conductor: 8.863398.86339
Root analytic conductor: 2.977142.97714
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ1110(961,⋅)\chi_{1110} (961, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 1110, ( :1/2), 0.444+0.895i)(2,\ 1110,\ (\ :1/2),\ 0.444 + 0.895i)

Particular Values

L(1)L(1) ≈\approx 1.2355351481.235535148
L(12)L(\frac12) ≈\approx 1.2355351481.235535148
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1−iT 1 - iT
3 1−T 1 - T
5 1+iT 1 + iT
37 1+(−2.70−5.44i)T 1 + (-2.70 - 5.44i)T
good7 1−0.374T+7T2 1 - 0.374T + 7T^{2}
11 1+6.11T+11T2 1 + 6.11T + 11T^{2}
13 1+5.44iT−13T2 1 + 5.44iT - 13T^{2}
17 1+2.37iT−17T2 1 + 2.37iT - 17T^{2}
19 1+1.70iT−19T2 1 + 1.70iT - 19T^{2}
23 1+5.44iT−23T2 1 + 5.44iT - 23T^{2}
29 1−4.41iT−29T2 1 - 4.41iT - 29T^{2}
31 1+3.07iT−31T2 1 + 3.07iT - 31T^{2}
41 1−3.07T+41T2 1 - 3.07T + 41T^{2}
43 1+7.82iT−43T2 1 + 7.82iT - 43T^{2}
47 1+13.3T+47T2 1 + 13.3T + 47T^{2}
53 1−2.37T+53T2 1 - 2.37T + 53T^{2}
59 1+10.8iT−59T2 1 + 10.8iT - 59T^{2}
61 1−4.07iT−61T2 1 - 4.07iT - 61T^{2}
67 1−10.1T+67T2 1 - 10.1T + 67T^{2}
71 1−4.74T+71T2 1 - 4.74T + 71T^{2}
73 1−8.19T+73T2 1 - 8.19T + 73T^{2}
79 1+12.1iT−79T2 1 + 12.1iT - 79T^{2}
83 1−6.78T+83T2 1 - 6.78T + 83T^{2}
89 1+0.551iT−89T2 1 + 0.551iT - 89T^{2}
97 1+8.15iT−97T2 1 + 8.15iT - 97T^{2}
show more
show less
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−9.643250500136900503648216274674, −8.527023911218116531486414470722, −8.077914705569534795624242974827, −7.48494037481886461616157557339, −6.36763560389966248533193120623, −5.13990249154716525426299727930, −4.93264080339173162798563934522, −3.37390782374923872688219762636, −2.45048548525437259149616380828, −0.48672693371614329752513174304, 1.75279153798382622683326816128, 2.61108377119400778804633141053, 3.61934492578378904858909251691, 4.57774513581011626737657588749, 5.59254541670223229303590087282, 6.74522537139669652952774237046, 7.82058160573652209554251003569, 8.248093614921785663155001568053, 9.472237342983389740511704198304, 9.863274838488575138934152885464

Graph of the ZZ-function along the critical line