↑

Properties

Label 2-1134-21.5-c1-0-6
Degree 22
Conductor 11341134
Sign −0.487−0.873i-0.487 - 0.873i
Analytic cond. 9.055039.05503
Root an. cond. 3.009153.00915
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

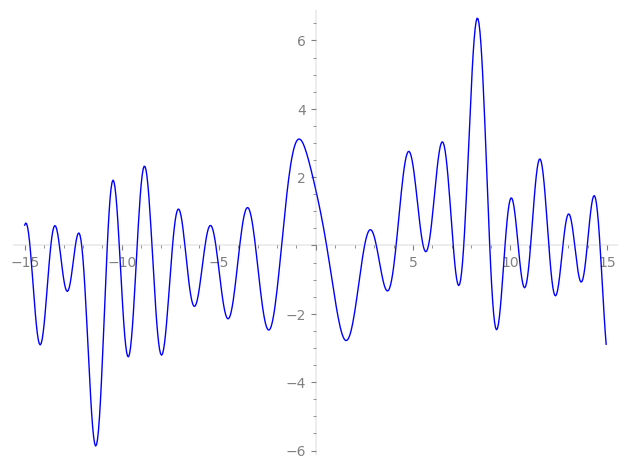
L(s)  = 1  + (0.866 + 0.5i)2-s + (0.499 + 0.866i)4-s + (0.450 − 0.779i)5-s + (−2.62 + 0.296i)7-s + 0.999i·8-s + (0.779 − 0.450i)10-s + (−2.70 + 1.56i)11-s + 2.29i·13-s + (−2.42 − 1.05i)14-s + (−0.5 + 0.866i)16-s + (2.57 + 4.46i)17-s + (2.38 + 1.37i)19-s + 0.900·20-s − 3.12·22-s + (−1.48 − 0.857i)23-s + ⋯
L(s)  = 1  + (0.612 + 0.353i)2-s + (0.249 + 0.433i)4-s + (0.201 − 0.348i)5-s + (−0.993 + 0.112i)7-s + 0.353i·8-s + (0.246 − 0.142i)10-s + (−0.816 + 0.471i)11-s + 0.637i·13-s + (−0.648 − 0.282i)14-s + (−0.125 + 0.216i)16-s + (0.624 + 1.08i)17-s + (0.546 + 0.315i)19-s + 0.201·20-s − 0.666·22-s + (−0.309 − 0.178i)23-s + ⋯

Functional equation

Λ(s)=(1134s/2 ΓC(s) L(s)=((−0.487−0.873i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 1134 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.487 - 0.873i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(1134s/2 ΓC(s+1/2) L(s)=((−0.487−0.873i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 1134 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.487 - 0.873i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 11341134    =    2⋅34⋅72 \cdot 3^{4} \cdot 7
Sign: −0.487−0.873i-0.487 - 0.873i
Analytic conductor: 9.055039.05503
Root analytic conductor: 3.009153.00915
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ1134(971,⋅)\chi_{1134} (971, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 1134, ( :1/2), −0.487−0.873i)(2,\ 1134,\ (\ :1/2),\ -0.487 - 0.873i)

Particular Values

L(1)L(1) ≈\approx 1.6124961841.612496184
L(12)L(\frac12) ≈\approx 1.6124961841.612496184
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(−0.866−0.5i)T 1 + (-0.866 - 0.5i)T
3 1 1
7 1+(2.62−0.296i)T 1 + (2.62 - 0.296i)T
good5 1+(−0.450+0.779i)T+(−2.5−4.33i)T2 1 + (-0.450 + 0.779i)T + (-2.5 - 4.33i)T^{2}
11 1+(2.70−1.56i)T+(5.5−9.52i)T2 1 + (2.70 - 1.56i)T + (5.5 - 9.52i)T^{2}
13 1−2.29iT−13T2 1 - 2.29iT - 13T^{2}
17 1+(−2.57−4.46i)T+(−8.5+14.7i)T2 1 + (-2.57 - 4.46i)T + (-8.5 + 14.7i)T^{2}
19 1+(−2.38−1.37i)T+(9.5+16.4i)T2 1 + (-2.38 - 1.37i)T + (9.5 + 16.4i)T^{2}
23 1+(1.48+0.857i)T+(11.5+19.9i)T2 1 + (1.48 + 0.857i)T + (11.5 + 19.9i)T^{2}
29 1−2.14iT−29T2 1 - 2.14iT - 29T^{2}
31 1+(8.66−5.00i)T+(15.5−26.8i)T2 1 + (8.66 - 5.00i)T + (15.5 - 26.8i)T^{2}
37 1+(4.73−8.20i)T+(−18.5−32.0i)T2 1 + (4.73 - 8.20i)T + (-18.5 - 32.0i)T^{2}
41 1−2.44T+41T2 1 - 2.44T + 41T^{2}
43 1−0.546T+43T2 1 - 0.546T + 43T^{2}
47 1+(−3.93+6.80i)T+(−23.5−40.7i)T2 1 + (-3.93 + 6.80i)T + (-23.5 - 40.7i)T^{2}
53 1+(−12.0+6.97i)T+(26.5−45.8i)T2 1 + (-12.0 + 6.97i)T + (26.5 - 45.8i)T^{2}
59 1+(−3.99−6.91i)T+(−29.5+51.0i)T2 1 + (-3.99 - 6.91i)T + (-29.5 + 51.0i)T^{2}
61 1+(6.28+3.62i)T+(30.5+52.8i)T2 1 + (6.28 + 3.62i)T + (30.5 + 52.8i)T^{2}
67 1+(1.83+3.17i)T+(−33.5+58.0i)T2 1 + (1.83 + 3.17i)T + (-33.5 + 58.0i)T^{2}
71 1+14.1iT−71T2 1 + 14.1iT - 71T^{2}
73 1+(10.9−6.30i)T+(36.5−63.2i)T2 1 + (10.9 - 6.30i)T + (36.5 - 63.2i)T^{2}
79 1+(−3.27+5.67i)T+(−39.5−68.4i)T2 1 + (-3.27 + 5.67i)T + (-39.5 - 68.4i)T^{2}
83 1−0.368T+83T2 1 - 0.368T + 83T^{2}
89 1+(6.00−10.3i)T+(−44.5−77.0i)T2 1 + (6.00 - 10.3i)T + (-44.5 - 77.0i)T^{2}
97 1−10.2iT−97T2 1 - 10.2iT - 97T^{2}
show more
show less
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.12794580574648473236675061707, −9.206425215636960151544062294430, −8.442922552033291447411521812741, −7.38336185633398085074446134693, −6.74707878490074682143338203472, −5.70982389755336639664348091219, −5.15416162332411380216659341377, −3.92302190667863973191657356313, −3.11766521277367553024933763863, −1.76703480821193348239996434520, 0.55097140676230452440329169381, 2.50746173863055204990334181303, 3.11354808998481474429968216383, 4.13061619961559064633220477550, 5.52370490206335629590936618343, 5.79752404335221283183794960601, 7.07358712923906120822873211348, 7.61477115340852376775612444464, 8.952780666251753766129729825372, 9.741259927841432134158453909525

Graph of the ZZ-function along the critical line