↑

Properties

Label 4-114e2-1.1-c5e2-0-0
Degree 44
Conductor 1299612996
Sign 11
Analytic cond. 334.295334.295
Root an. cond. 4.275954.27595
Motivic weight 55
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 8·2-s + 18·3-s + 48·4-s − 49·5-s − 144·6-s − 105·7-s − 256·8-s + 243·9-s + 392·10-s + 725·11-s + 864·12-s − 56·13-s + 840·14-s − 882·15-s + 1.28e3·16-s + 1.52e3·17-s − 1.94e3·18-s − 722·19-s − 2.35e3·20-s − 1.89e3·21-s − 5.80e3·22-s + 1.70e3·23-s − 4.60e3·24-s − 3.42e3·25-s + 448·26-s + 2.91e3·27-s − 5.04e3·28-s + ⋯
L(s)  = 1  − 1.41·2-s + 1.15·3-s + 3/2·4-s − 0.876·5-s − 1.63·6-s − 0.809·7-s − 1.41·8-s + 9-s + 1.23·10-s + 1.80·11-s + 1.73·12-s − 0.0919·13-s + 1.14·14-s − 1.01·15-s + 5/4·16-s + 1.27·17-s − 1.41·18-s − 0.458·19-s − 1.31·20-s − 0.935·21-s − 2.55·22-s + 0.670·23-s − 1.63·24-s − 1.09·25-s + 0.129·26-s + 0.769·27-s − 1.21·28-s + ⋯

Functional equation

Λ(s)=(12996s/2 ΓC(s)2 L(s)=( Λ(6−s)\begin{aligned}\Lambda(s)=\mathstrut & 12996 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(6-s) \end{aligned}
Λ(s)=(12996s/2 ΓC(s+5/2)2 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 12996 ^{s/2} \, \Gamma_{\C}(s+5/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 44
Conductor: 1299612996    =    22⋅32⋅1922^{2} \cdot 3^{2} \cdot 19^{2}
Sign: 11
Analytic conductor: 334.295334.295
Root analytic conductor: 4.275954.27595
Motivic weight: 55
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (4, 12996, ( :5/2,5/2), 1)(4,\ 12996,\ (\ :5/2, 5/2),\ 1)

Particular Values

L(3)L(3) ≈\approx 2.2135470652.213547065
L(12)L(\frac12) ≈\approx 2.2135470652.213547065
L(72)L(\frac{7}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2C1C_1 (1+p2T)2 ( 1 + p^{2} T )^{2}
3C1C_1 (1−p2T)2 ( 1 - p^{2} T )^{2}
19C1C_1 (1+p2T)2 ( 1 + p^{2} T )^{2}
good5D4D_{4} 1+49T+5828T2+49p5T3+p10T4 1 + 49 T + 5828 T^{2} + 49 p^{5} T^{3} + p^{10} T^{4}
7D4D_{4} 1+15pT+10814T2+15p6T3+p10T4 1 + 15 p T + 10814 T^{2} + 15 p^{6} T^{3} + p^{10} T^{4}
11D4D_{4} 1−725T+452486T2−725p5T3+p10T4 1 - 725 T + 452486 T^{2} - 725 p^{5} T^{3} + p^{10} T^{4}
13D4D_{4} 1+56T+334470T2+56p5T3+p10T4 1 + 56 T + 334470 T^{2} + 56 p^{5} T^{3} + p^{10} T^{4}
17D4D_{4} 1−1521T+1863232T2−1521p5T3+p10T4 1 - 1521 T + 1863232 T^{2} - 1521 p^{5} T^{3} + p^{10} T^{4}
23D4D_{4} 1−1700T−160210T2−1700p5T3+p10T4 1 - 1700 T - 160210 T^{2} - 1700 p^{5} T^{3} + p^{10} T^{4}
29D4D_{4} 1−12724T+81235646T2−12724p5T3+p10T4 1 - 12724 T + 81235646 T^{2} - 12724 p^{5} T^{3} + p^{10} T^{4}
31D4D_{4} 1−8558T+58292118T2−8558p5T3+p10T4 1 - 8558 T + 58292118 T^{2} - 8558 p^{5} T^{3} + p^{10} T^{4}
37D4D_{4} 1−12434T+135627114T2−12434p5T3+p10T4 1 - 12434 T + 135627114 T^{2} - 12434 p^{5} T^{3} + p^{10} T^{4}
41D4D_{4} 1−20230T+259503602T2−20230p5T3+p10T4 1 - 20230 T + 259503602 T^{2} - 20230 p^{5} T^{3} + p^{10} T^{4}
43D4D_{4} 1−4895T+299556330T2−4895p5T3+p10T4 1 - 4895 T + 299556330 T^{2} - 4895 p^{5} T^{3} + p^{10} T^{4}
47D4D_{4} 1−21059T+555084302T2−21059p5T3+p10T4 1 - 21059 T + 555084302 T^{2} - 21059 p^{5} T^{3} + p^{10} T^{4}
53D4D_{4} 1−25196T+966248606T2−25196p5T3+p10T4 1 - 25196 T + 966248606 T^{2} - 25196 p^{5} T^{3} + p^{10} T^{4}
59D4D_{4} 1−1560T+1429410214T2−1560p5T3+p10T4 1 - 1560 T + 1429410214 T^{2} - 1560 p^{5} T^{3} + p^{10} T^{4}
61D4D_{4} 1+2123T−588325956T2+2123p5T3+p10T4 1 + 2123 T - 588325956 T^{2} + 2123 p^{5} T^{3} + p^{10} T^{4}
67D4D_{4} 1+46968T+3250701686T2+46968p5T3+p10T4 1 + 46968 T + 3250701686 T^{2} + 46968 p^{5} T^{3} + p^{10} T^{4}
71D4D_{4} 1−60056T+2271003086T2−60056p5T3+p10T4 1 - 60056 T + 2271003086 T^{2} - 60056 p^{5} T^{3} + p^{10} T^{4}
73D4D_{4} 1+57177T+4702746212T2+57177p5T3+p10T4 1 + 57177 T + 4702746212 T^{2} + 57177 p^{5} T^{3} + p^{10} T^{4}
79D4D_{4} 1+99368T+8517934254T2+99368p5T3+p10T4 1 + 99368 T + 8517934254 T^{2} + 99368 p^{5} T^{3} + p^{10} T^{4}
83D4D_{4} 1+21780T−3626701658T2+21780p5T3+p10T4 1 + 21780 T - 3626701658 T^{2} + 21780 p^{5} T^{3} + p^{10} T^{4}
89D4D_{4} 1+11856T+2415361198T2+11856p5T3+p10T4 1 + 11856 T + 2415361198 T^{2} + 11856 p^{5} T^{3} + p^{10} T^{4}
97D4D_{4} 1+77068T−559666266T2+77068p5T3+p10T4 1 + 77068 T - 559666266 T^{2} + 77068 p^{5} T^{3} + p^{10} T^{4}
show more
show less
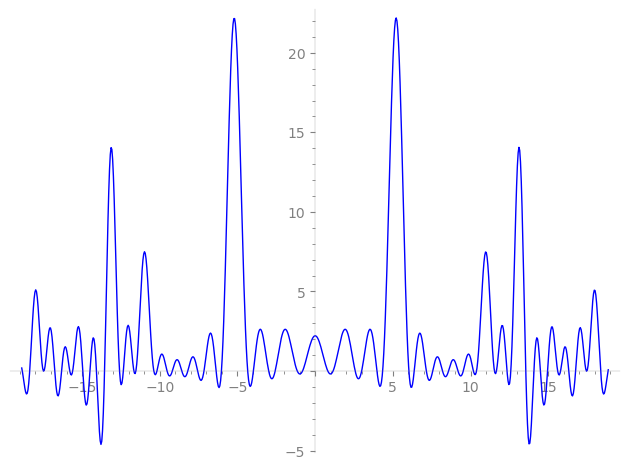
   L(s)=∏p ∏j=14(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−12.59077662442301502535017374809, −12.34699905643317480108195750971, −11.66689302118222171502422080708, −11.53877921073748755680088974846, −10.38404933270753762296681404857, −10.18348210530864781605951302574, −9.532086136105657560223432370297, −9.191725621198016247111052480499, −8.583966024772736185898767506845, −8.196511280388750974797120557625, −7.56581412496507055927749357261, −7.15622885548722860066789836077, −6.37570646886252990644723498936, −6.03295358005877565783144992649, −4.34245187045827182781694863796, −3.97500465481077572317087483570, −2.99102723988132078536658953077, −2.57445413174859067452073381954, −1.15250050606863482145280041400, −0.812121560386603378916570811270, 0.812121560386603378916570811270, 1.15250050606863482145280041400, 2.57445413174859067452073381954, 2.99102723988132078536658953077, 3.97500465481077572317087483570, 4.34245187045827182781694863796, 6.03295358005877565783144992649, 6.37570646886252990644723498936, 7.15622885548722860066789836077, 7.56581412496507055927749357261, 8.196511280388750974797120557625, 8.583966024772736185898767506845, 9.191725621198016247111052480499, 9.532086136105657560223432370297, 10.18348210530864781605951302574, 10.38404933270753762296681404857, 11.53877921073748755680088974846, 11.66689302118222171502422080708, 12.34699905643317480108195750971, 12.59077662442301502535017374809

Graph of the ZZ-function along the critical line