↑

Properties

Label 2-1320-1320.413-c0-0-3
Degree $2$
Conductor $1320$
Sign $-0.995 + 0.0965i$
Analytic cond. $0.658765$
Root an. cond. $0.811643$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.453 − 0.891i)2-s + (−0.156 − 0.987i)3-s + (−0.587 − 0.809i)4-s + (0.156 − 0.987i)5-s + (−0.951 − 0.309i)6-s + (0.896 + 0.142i)7-s + (−0.987 + 0.156i)8-s + (−0.951 + 0.309i)9-s + (−0.809 − 0.587i)10-s + (0.707 − 0.707i)11-s + (−0.707 + 0.707i)12-s + (0.533 − 0.734i)14-s − 15-s + (−0.309 + 0.951i)16-s + (−0.156 + 0.987i)18-s + ⋯
L(s)  = 1  + (0.453 − 0.891i)2-s + (−0.156 − 0.987i)3-s + (−0.587 − 0.809i)4-s + (0.156 − 0.987i)5-s + (−0.951 − 0.309i)6-s + (0.896 + 0.142i)7-s + (−0.987 + 0.156i)8-s + (−0.951 + 0.309i)9-s + (−0.809 − 0.587i)10-s + (0.707 − 0.707i)11-s + (−0.707 + 0.707i)12-s + (0.533 − 0.734i)14-s − 15-s + (−0.309 + 0.951i)16-s + (−0.156 + 0.987i)18-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 1320 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.995 + 0.0965i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 1320 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.995 + 0.0965i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(1320\)    =    \(2^{3} \cdot 3 \cdot 5 \cdot 11\)
Sign: $-0.995 + 0.0965i$
Analytic conductor: \(0.658765\)
Root analytic conductor: \(0.811643\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{1320} (413, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 1320,\ (\ :0),\ -0.995 + 0.0965i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.293897352\)
\(L(\frac12)\) \(\approx\) \(1.293897352\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (-0.453 + 0.891i)T \)
3 \( 1 + (0.156 + 0.987i)T \)
5 \( 1 + (-0.156 + 0.987i)T \)
11 \( 1 + (-0.707 + 0.707i)T \)
good7 \( 1 + (-0.896 - 0.142i)T + (0.951 + 0.309i)T^{2} \)
13 \( 1 + (-0.587 - 0.809i)T^{2} \)
17 \( 1 + (-0.587 + 0.809i)T^{2} \)
19 \( 1 + (-0.309 - 0.951i)T^{2} \)
23 \( 1 - iT^{2} \)
29 \( 1 + (0.253 - 0.183i)T + (0.309 - 0.951i)T^{2} \)
31 \( 1 + (-0.587 - 1.80i)T + (-0.809 + 0.587i)T^{2} \)
37 \( 1 + (0.951 + 0.309i)T^{2} \)
41 \( 1 + (0.309 + 0.951i)T^{2} \)
43 \( 1 + iT^{2} \)
47 \( 1 + (-0.951 + 0.309i)T^{2} \)
53 \( 1 + (0.280 - 0.550i)T + (-0.587 - 0.809i)T^{2} \)
59 \( 1 + (-1.04 - 1.44i)T + (-0.309 + 0.951i)T^{2} \)
61 \( 1 + (-0.809 - 0.587i)T^{2} \)
67 \( 1 + iT^{2} \)
71 \( 1 + (0.809 + 0.587i)T^{2} \)
73 \( 1 + (-0.309 + 1.95i)T + (-0.951 - 0.309i)T^{2} \)
79 \( 1 + (-0.5 - 1.53i)T + (-0.809 + 0.587i)T^{2} \)
83 \( 1 + (0.734 + 1.44i)T + (-0.587 + 0.809i)T^{2} \)
89 \( 1 + T^{2} \)
97 \( 1 + (1.76 + 0.896i)T + (0.587 + 0.809i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

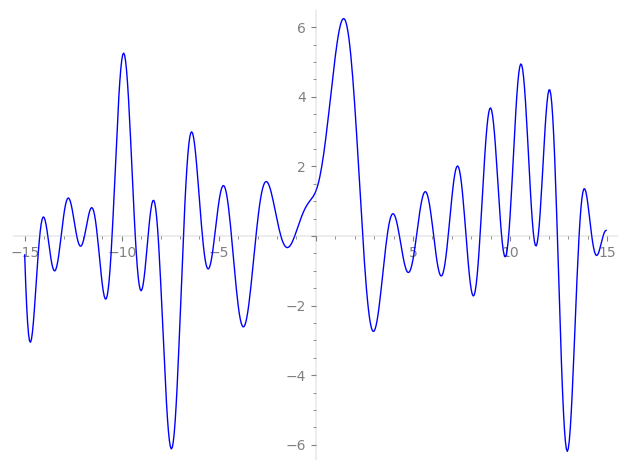
Imaginary part of the first few zeros on the critical line

−9.304043539756123159121813115712, −8.643946271870561136163212080382, −8.128127597756525706585917678597, −6.82370383503027853585408188821, −5.84614363120418028573579428899, −5.21535077798277189477024831855, −4.34893624421944344836003945311, −3.08699768363626840554484186772, −1.80507312353087248848677387087, −1.09072612856837774498989076706, 2.41048268212136326529470636377, 3.66853739311702328132848032959, 4.30268763872519183977617838696, 5.18042097097884608939218214146, 6.06761955766815337044080302134, 6.81307415233890380188367944981, 7.73412055932866845395637101310, 8.453694666267075156775904370822, 9.566792617391321665404064092960, 9.926661367629454239054133172646

Graph of the $Z$-function along the critical line