↑

Properties

Label 2-2e4-1.1-c27-0-10
Degree 22
Conductor 1616
Sign 11
Analytic cond. 73.896873.8968
Root an. cond. 8.596338.59633
Motivic weight 2727
Arithmetic yes
Rational no
Primitive yes
Self-dual yes
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 4.98e6·3-s + 3.10e9·5-s + 2.36e11·7-s + 1.72e13·9-s + 2.12e14·11-s − 1.46e15·13-s + 1.54e16·15-s + 2.34e15·17-s + 9.03e16·19-s + 1.17e18·21-s − 1.52e18·23-s + 2.18e18·25-s + 4.77e19·27-s + 1.80e19·29-s − 3.08e19·31-s + 1.05e21·33-s + 7.33e20·35-s − 6.43e20·37-s − 7.32e21·39-s − 7.21e21·41-s − 1.26e22·43-s + 5.34e22·45-s − 6.23e22·47-s − 9.79e21·49-s + 1.16e22·51-s + 1.22e23·53-s + 6.59e23·55-s + ⋯
L(s)  = 1  + 1.80·3-s + 1.13·5-s + 0.922·7-s + 2.25·9-s + 1.85·11-s − 1.34·13-s + 2.05·15-s + 0.0574·17-s + 0.492·19-s + 1.66·21-s − 0.631·23-s + 0.292·25-s + 2.26·27-s + 0.326·29-s − 0.226·31-s + 3.34·33-s + 1.04·35-s − 0.434·37-s − 2.42·39-s − 1.21·41-s − 1.11·43-s + 2.56·45-s − 1.66·47-s − 0.149·49-s + 0.103·51-s + 0.646·53-s + 2.10·55-s + ⋯

Functional equation

Λ(s)=(16s/2 ΓC(s) L(s)=( Λ(28−s)\begin{aligned}\Lambda(s)=\mathstrut & 16 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & \, \Lambda(28-s) \end{aligned}
Λ(s)=(16s/2 ΓC(s+27/2) L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 16 ^{s/2} \, \Gamma_{\C}(s+27/2) \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 1616    =    242^{4}
Sign: 11
Analytic conductor: 73.896873.8968
Root analytic conductor: 8.596338.59633
Motivic weight: 2727
Rational: no
Arithmetic: yes
Character: Trivial
Primitive: yes
Self-dual: yes
Analytic rank: 00
Selberg data: (2, 16, ( :27/2), 1)(2,\ 16,\ (\ :27/2),\ 1)

Particular Values

L(14)L(14) ≈\approx 6.4695672156.469567215
L(12)L(\frac12) ≈\approx 6.4695672156.469567215
L(292)L(\frac{29}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
good3 1−4.98e6T+7.62e12T2 1 - 4.98e6T + 7.62e12T^{2}
5 1−3.10e9T+7.45e18T2 1 - 3.10e9T + 7.45e18T^{2}
7 1−2.36e11T+6.57e22T2 1 - 2.36e11T + 6.57e22T^{2}
11 1−2.12e14T+1.31e28T2 1 - 2.12e14T + 1.31e28T^{2}
13 1+1.46e15T+1.19e30T2 1 + 1.46e15T + 1.19e30T^{2}
17 1−2.34e15T+1.66e33T2 1 - 2.34e15T + 1.66e33T^{2}
19 1−9.03e16T+3.36e34T2 1 - 9.03e16T + 3.36e34T^{2}
23 1+1.52e18T+5.84e36T2 1 + 1.52e18T + 5.84e36T^{2}
29 1−1.80e19T+3.05e39T2 1 - 1.80e19T + 3.05e39T^{2}
31 1+3.08e19T+1.84e40T2 1 + 3.08e19T + 1.84e40T^{2}
37 1+6.43e20T+2.19e42T2 1 + 6.43e20T + 2.19e42T^{2}
41 1+7.21e21T+3.50e43T2 1 + 7.21e21T + 3.50e43T^{2}
43 1+1.26e22T+1.26e44T2 1 + 1.26e22T + 1.26e44T^{2}
47 1+6.23e22T+1.40e45T2 1 + 6.23e22T + 1.40e45T^{2}
53 1−1.22e23T+3.59e46T2 1 - 1.22e23T + 3.59e46T^{2}
59 1+1.26e24T+6.50e47T2 1 + 1.26e24T + 6.50e47T^{2}
61 1+4.90e23T+1.59e48T2 1 + 4.90e23T + 1.59e48T^{2}
67 1−2.60e24T+2.01e49T2 1 - 2.60e24T + 2.01e49T^{2}
71 1+7.66e24T+9.63e49T2 1 + 7.66e24T + 9.63e49T^{2}
73 1−2.19e25T+2.04e50T2 1 - 2.19e25T + 2.04e50T^{2}
79 1−7.76e25T+1.72e51T2 1 - 7.76e25T + 1.72e51T^{2}
83 1+3.00e25T+6.53e51T2 1 + 3.00e25T + 6.53e51T^{2}
89 1−2.29e26T+4.30e52T2 1 - 2.29e26T + 4.30e52T^{2}
97 1+1.71e26T+4.39e53T2 1 + 1.71e26T + 4.39e53T^{2}
show more
show less
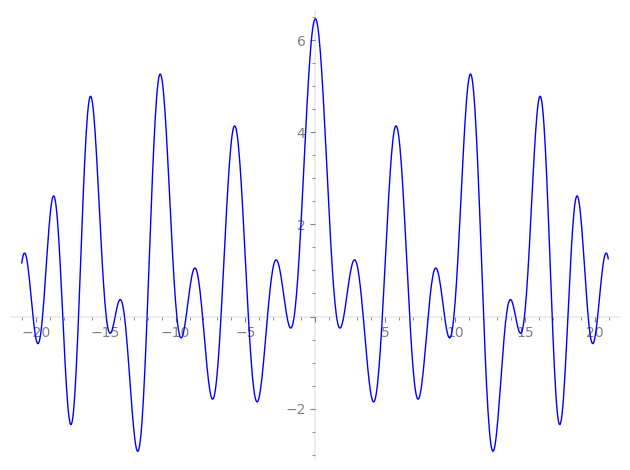
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−13.65135218437225710582321850655, −12.03413052079825843817815850242, −9.907111154658323456103239024973, −9.243636028279992175944653782056, −8.067270190111903599253911599863, −6.74721177642138430341489504585, −4.79051127184189824090222370309, −3.42314905000503201273184687042, −2.03103965597371932695249098477, −1.51508517941992458298148864352, 1.51508517941992458298148864352, 2.03103965597371932695249098477, 3.42314905000503201273184687042, 4.79051127184189824090222370309, 6.74721177642138430341489504585, 8.067270190111903599253911599863, 9.243636028279992175944653782056, 9.907111154658323456103239024973, 12.03413052079825843817815850242, 13.65135218437225710582321850655

Graph of the ZZ-function along the critical line