↑

Properties

Label 2-171-57.56-c1-0-4
Degree 22
Conductor 171171
Sign 0.577+0.816i0.577 + 0.816i
Analytic cond. 1.365441.36544
Root an. cond. 1.168521.16852
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

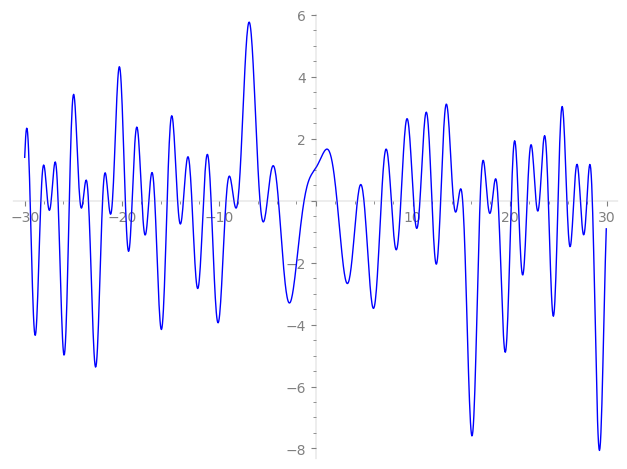
L(s)  = 1  − 2·4-s − 2.37i·5-s + 4.35·7-s − 6.61i·11-s + 4·16-s + 1.86i·17-s − 4.35·19-s + 4.75i·20-s + 8.99i·23-s − 0.641·25-s − 8.71·28-s − 10.3i·35-s − 43-s + 13.2i·44-s + 6.11i·47-s + ⋯
L(s)  = 1  − 4-s − 1.06i·5-s + 1.64·7-s − 1.99i·11-s + 16-s + 0.452i·17-s − 1.00·19-s + 1.06i·20-s + 1.87i·23-s − 0.128·25-s − 1.64·28-s − 1.74i·35-s − 0.152·43-s + 1.99i·44-s + 0.891i·47-s + ⋯

Functional equation

Λ(s)=(171s/2 ΓC(s) L(s)=((0.577+0.816i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 171 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.577 + 0.816i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(171s/2 ΓC(s+1/2) L(s)=((0.577+0.816i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 171 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.577 + 0.816i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 171171    =    32⋅193^{2} \cdot 19
Sign: 0.577+0.816i0.577 + 0.816i
Analytic conductor: 1.365441.36544
Root analytic conductor: 1.168521.16852
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ171(170,⋅)\chi_{171} (170, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 171, ( :1/2), 0.577+0.816i)(2,\ 171,\ (\ :1/2),\ 0.577 + 0.816i)

Particular Values

L(1)L(1) ≈\approx 0.931848−0.482360i0.931848 - 0.482360i
L(12)L(\frac12) ≈\approx 0.931848−0.482360i0.931848 - 0.482360i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad3 1 1
19 1+4.35T 1 + 4.35T
good2 1+2T2 1 + 2T^{2}
5 1+2.37iT−5T2 1 + 2.37iT - 5T^{2}
7 1−4.35T+7T2 1 - 4.35T + 7T^{2}
11 1+6.61iT−11T2 1 + 6.61iT - 11T^{2}
13 1−13T2 1 - 13T^{2}
17 1−1.86iT−17T2 1 - 1.86iT - 17T^{2}
23 1−8.99iT−23T2 1 - 8.99iT - 23T^{2}
29 1+29T2 1 + 29T^{2}
31 1−31T2 1 - 31T^{2}
37 1−37T2 1 - 37T^{2}
41 1+41T2 1 + 41T^{2}
43 1+T+43T2 1 + T + 43T^{2}
47 1−6.11iT−47T2 1 - 6.11iT - 47T^{2}
53 1+53T2 1 + 53T^{2}
59 1+59T2 1 + 59T^{2}
61 1−4.35T+61T2 1 - 4.35T + 61T^{2}
67 1−67T2 1 - 67T^{2}
71 1+71T2 1 + 71T^{2}
73 1−11T+73T2 1 - 11T + 73T^{2}
79 1−79T2 1 - 79T^{2}
83 1−17.4iT−83T2 1 - 17.4iT - 83T^{2}
89 1+89T2 1 + 89T^{2}
97 1−97T2 1 - 97T^{2}
show more
show less
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−12.76832591629747791780056268042, −11.56702058787996924257041615799, −10.78807663601031237718037695283, −9.245015387463118943826530040374, −8.433774734769499447297411708611, −8.022828193466520071020103123035, −5.74748405417098613937629589742, −4.99029040060361356124191245892, −3.84244602729586642983218618364, −1.19761556299323890853626080839, 2.19220898156498664547707092403, 4.30063438461480201546142650044, 4.96946250265873615426572728138, 6.76307186717429580077078497625, 7.79174925641288207389001775538, 8.776685635403250871995095011550, 10.08470214758574881223163686046, 10.74304417909708818750143435461, 11.97359450962457679771706702162, 12.87535129756270034798468957719

Graph of the ZZ-function along the critical line