↑

Properties

Label 2-220-5.4-c5-0-21
Degree 22
Conductor 220220
Sign 0.228+0.973i0.228 + 0.973i
Analytic cond. 35.284435.2844
Root an. cond. 5.940075.94007
Motivic weight 55
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 26.2i·3-s + (12.7 + 54.4i)5-s − 64.0i·7-s − 443.·9-s + 121·11-s − 528. i·13-s + (−1.42e3 + 335. i)15-s − 1.54e3i·17-s − 3.10e3·19-s + 1.67e3·21-s − 1.78e3i·23-s + (−2.79e3 + 1.39e3i)25-s − 5.26e3i·27-s − 4.89e3·29-s + 1.17e3·31-s + ⋯
L(s)  = 1  + 1.68i·3-s + (0.228 + 0.973i)5-s − 0.494i·7-s − 1.82·9-s + 0.301·11-s − 0.867i·13-s + (−1.63 + 0.384i)15-s − 1.29i·17-s − 1.97·19-s + 0.831·21-s − 0.705i·23-s + (−0.895 + 0.445i)25-s − 1.38i·27-s − 1.08·29-s + 0.219·31-s + ⋯

Functional equation

Λ(s)=(220s/2 ΓC(s) L(s)=((0.228+0.973i) Λ‾(6−s)\begin{aligned}\Lambda(s)=\mathstrut & 220 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.228 + 0.973i)\, \overline{\Lambda}(6-s) \end{aligned}
Λ(s)=(220s/2 ΓC(s+5/2) L(s)=((0.228+0.973i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 220 ^{s/2} \, \Gamma_{\C}(s+5/2) \, L(s)\cr =\mathstrut & (0.228 + 0.973i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 220220    =    22⋅5⋅112^{2} \cdot 5 \cdot 11
Sign: 0.228+0.973i0.228 + 0.973i
Analytic conductor: 35.284435.2844
Root analytic conductor: 5.940075.94007
Motivic weight: 55
Rational: no
Arithmetic: yes
Character: χ220(89,⋅)\chi_{220} (89, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 220, ( :5/2), 0.228+0.973i)(2,\ 220,\ (\ :5/2),\ 0.228 + 0.973i)

Particular Values

L(3)L(3) ≈\approx 0.12579919120.1257991912
L(12)L(\frac12) ≈\approx 0.12579919120.1257991912
L(72)L(\frac{7}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
5 1+(−12.7−54.4i)T 1 + (-12.7 - 54.4i)T
11 1−121T 1 - 121T
good3 1−26.2iT−243T2 1 - 26.2iT - 243T^{2}
7 1+64.0iT−1.68e4T2 1 + 64.0iT - 1.68e4T^{2}
13 1+528.iT−3.71e5T2 1 + 528. iT - 3.71e5T^{2}
17 1+1.54e3iT−1.41e6T2 1 + 1.54e3iT - 1.41e6T^{2}
19 1+3.10e3T+2.47e6T2 1 + 3.10e3T + 2.47e6T^{2}
23 1+1.78e3iT−6.43e6T2 1 + 1.78e3iT - 6.43e6T^{2}
29 1+4.89e3T+2.05e7T2 1 + 4.89e3T + 2.05e7T^{2}
31 1−1.17e3T+2.86e7T2 1 - 1.17e3T + 2.86e7T^{2}
37 1−1.26e4iT−6.93e7T2 1 - 1.26e4iT - 6.93e7T^{2}
41 1−1.52e3T+1.15e8T2 1 - 1.52e3T + 1.15e8T^{2}
43 1+1.15e4iT−1.47e8T2 1 + 1.15e4iT - 1.47e8T^{2}
47 1+1.97e4iT−2.29e8T2 1 + 1.97e4iT - 2.29e8T^{2}
53 1−1.62e4iT−4.18e8T2 1 - 1.62e4iT - 4.18e8T^{2}
59 1+3.94e4T+7.14e8T2 1 + 3.94e4T + 7.14e8T^{2}
61 1−1.88e4T+8.44e8T2 1 - 1.88e4T + 8.44e8T^{2}
67 1−4.04e4iT−1.35e9T2 1 - 4.04e4iT - 1.35e9T^{2}
71 1+6.52e4T+1.80e9T2 1 + 6.52e4T + 1.80e9T^{2}
73 1+4.63e4iT−2.07e9T2 1 + 4.63e4iT - 2.07e9T^{2}
79 1−2.01e4T+3.07e9T2 1 - 2.01e4T + 3.07e9T^{2}
83 1−8.59e4iT−3.93e9T2 1 - 8.59e4iT - 3.93e9T^{2}
89 1+1.20e4T+5.58e9T2 1 + 1.20e4T + 5.58e9T^{2}
97 1+1.37e5iT−8.58e9T2 1 + 1.37e5iT - 8.58e9T^{2}
show more
show less
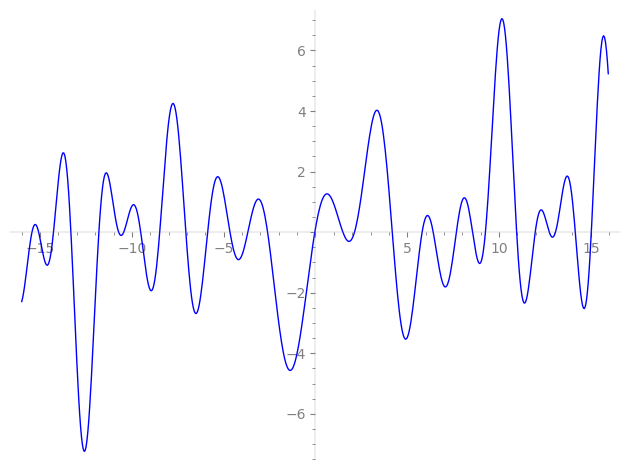
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.71884116915888744290315104296, −10.44439392925725388534174089090, −9.518127325479863721122990604124, −8.483923255494046631432929848002, −7.06072265045491266602158159483, −5.87291305896101077764680554704, −4.65517925568218560936373972014, −3.68356943561501691654136554155, −2.60713839568317739207525011394, −0.03508440682371567314721820898, 1.49419607824154743958717521482, 2.12613273853625183774241182471, 4.18433960833391905576088502868, 5.81034520946496049619229421086, 6.41420536354077558026002965468, 7.67513888258630631453653702941, 8.556786906066278736230702814719, 9.258182914359376951987978095431, 10.95888388135685110107767865941, 11.97139858534285079010151998906

Graph of the ZZ-function along the critical line