↑

Properties

Label 2-2303-2303.939-c0-0-4
Degree $2$
Conductor $2303$
Sign $0.582 + 0.812i$
Analytic cond. $1.14934$
Root an. cond. $1.07207$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.385 + 0.483i)2-s + (0.708 − 0.341i)3-s + (0.137 − 0.602i)4-s + (0.437 + 0.210i)6-s + (−0.550 − 0.834i)7-s + (0.900 − 0.433i)8-s + (−0.238 + 0.298i)9-s + (−0.108 − 0.473i)12-s + (0.190 − 0.587i)14-s + (−0.437 − 1.91i)17-s − 0.236·18-s + (−0.674 − 0.403i)21-s + (0.490 − 0.614i)24-s + (0.623 − 0.781i)25-s + (−0.241 + 1.05i)27-s + (−0.578 + 0.217i)28-s + ⋯
L(s)  = 1  + (0.385 + 0.483i)2-s + (0.708 − 0.341i)3-s + (0.137 − 0.602i)4-s + (0.437 + 0.210i)6-s + (−0.550 − 0.834i)7-s + (0.900 − 0.433i)8-s + (−0.238 + 0.298i)9-s + (−0.108 − 0.473i)12-s + (0.190 − 0.587i)14-s + (−0.437 − 1.91i)17-s − 0.236·18-s + (−0.674 − 0.403i)21-s + (0.490 − 0.614i)24-s + (0.623 − 0.781i)25-s + (−0.241 + 1.05i)27-s + (−0.578 + 0.217i)28-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 2303 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.582 + 0.812i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2303 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.582 + 0.812i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(2303\)    =    \(7^{2} \cdot 47\)
Sign: $0.582 + 0.812i$
Analytic conductor: \(1.14934\)
Root analytic conductor: \(1.07207\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{2303} (939, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 2303,\ (\ :0),\ 0.582 + 0.812i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.762790037\)
\(L(\frac12)\) \(\approx\) \(1.762790037\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad7 \( 1 + (0.550 + 0.834i)T \)
47 \( 1 + (-0.623 - 0.781i)T \)
good2 \( 1 + (-0.385 - 0.483i)T + (-0.222 + 0.974i)T^{2} \)
3 \( 1 + (-0.708 + 0.341i)T + (0.623 - 0.781i)T^{2} \)
5 \( 1 + (-0.623 + 0.781i)T^{2} \)
11 \( 1 + (0.222 - 0.974i)T^{2} \)
13 \( 1 + (0.222 - 0.974i)T^{2} \)
17 \( 1 + (0.437 + 1.91i)T + (-0.900 + 0.433i)T^{2} \)
19 \( 1 - T^{2} \)
23 \( 1 + (0.900 + 0.433i)T^{2} \)
29 \( 1 + (0.900 - 0.433i)T^{2} \)
31 \( 1 - T^{2} \)
37 \( 1 + (-0.429 - 1.87i)T + (-0.900 + 0.433i)T^{2} \)
41 \( 1 + (-0.623 + 0.781i)T^{2} \)
43 \( 1 + (-0.623 - 0.781i)T^{2} \)
53 \( 1 + (0.382 - 1.67i)T + (-0.900 - 0.433i)T^{2} \)
59 \( 1 + (-1.24 - 0.599i)T + (0.623 + 0.781i)T^{2} \)
61 \( 1 + (0.416 + 1.82i)T + (-0.900 + 0.433i)T^{2} \)
67 \( 1 - T^{2} \)
71 \( 1 + (-0.174 + 0.766i)T + (-0.900 - 0.433i)T^{2} \)
73 \( 1 + (0.222 + 0.974i)T^{2} \)
79 \( 1 - 0.947T + T^{2} \)
83 \( 1 + (0.277 - 0.347i)T + (-0.222 - 0.974i)T^{2} \)
89 \( 1 + (-0.385 + 0.483i)T + (-0.222 - 0.974i)T^{2} \)
97 \( 1 - 0.618T + T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

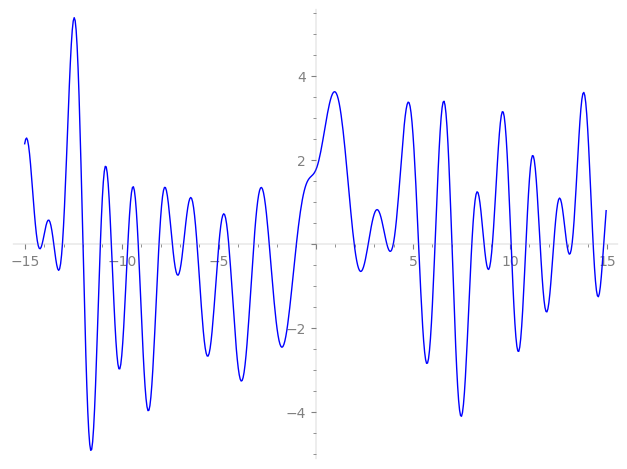
Imaginary part of the first few zeros on the critical line

−9.152609853406232742107727603890, −8.080807149102222040025702266315, −7.39415848666228967288461796149, −6.81842095028109360437194408407, −6.12364731473370043704973415363, −4.99718922773366558875485119500, −4.49122203718087769088710745735, −3.19680946232453016208377440169, −2.40392279372308042359341831534, −1.00423766740494491729012477061, 1.97194515513467837255925467401, 2.69619479397757732159364510172, 3.65190466843018323311321176815, 3.98758122759132627073675584944, 5.28810086975675907860435298883, 6.13716963849216008039524924649, 7.00677322438659286275154354628, 8.031700284358141728320270060571, 8.661683946213194744827706028966, 9.090889299717543807047256839645

Graph of the $Z$-function along the critical line