↑

Properties

Label 2-3042-13.12-c1-0-34
Degree 22
Conductor 30423042
Sign 0.960−0.277i0.960 - 0.277i
Analytic cond. 24.290424.2904
Root an. cond. 4.928534.92853
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

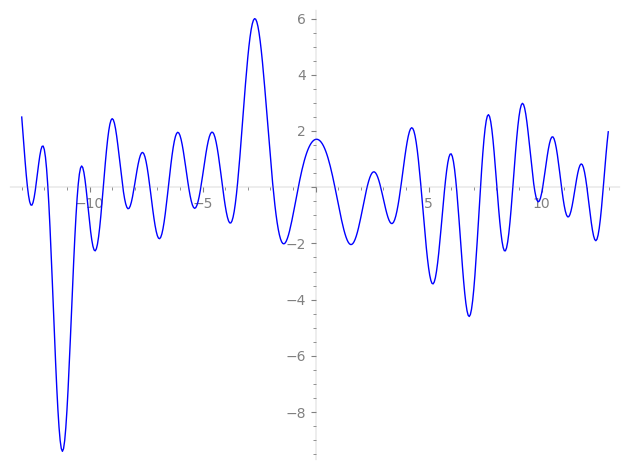
L(s)  = 1  + i·2-s − 4-s − 1.73i·5-s − 1.26i·7-s − i·8-s + 1.73·10-s + 1.26i·11-s + 1.26·14-s + 16-s + 5.19·17-s + 4.73i·19-s + 1.73i·20-s − 1.26·22-s − 8.19·23-s + 2.00·25-s + ⋯
L(s)  = 1  + 0.707i·2-s − 0.5·4-s − 0.774i·5-s − 0.479i·7-s − 0.353i·8-s + 0.547·10-s + 0.382i·11-s + 0.338·14-s + 0.250·16-s + 1.26·17-s + 1.08i·19-s + 0.387i·20-s − 0.270·22-s − 1.70·23-s + 0.400·25-s + ⋯

Functional equation

Λ(s)=(3042s/2 ΓC(s) L(s)=((0.960−0.277i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 3042 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.960 - 0.277i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(3042s/2 ΓC(s+1/2) L(s)=((0.960−0.277i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 3042 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.960 - 0.277i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 30423042    =    2⋅32⋅1322 \cdot 3^{2} \cdot 13^{2}
Sign: 0.960−0.277i0.960 - 0.277i
Analytic conductor: 24.290424.2904
Root analytic conductor: 4.928534.92853
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ3042(1351,⋅)\chi_{3042} (1351, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 3042, ( :1/2), 0.960−0.277i)(2,\ 3042,\ (\ :1/2),\ 0.960 - 0.277i)

Particular Values

L(1)L(1) ≈\approx 1.7008170381.700817038
L(12)L(\frac12) ≈\approx 1.7008170381.700817038
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1−iT 1 - iT
3 1 1
13 1 1
good5 1+1.73iT−5T2 1 + 1.73iT - 5T^{2}
7 1+1.26iT−7T2 1 + 1.26iT - 7T^{2}
11 1−1.26iT−11T2 1 - 1.26iT - 11T^{2}
17 1−5.19T+17T2 1 - 5.19T + 17T^{2}
19 1−4.73iT−19T2 1 - 4.73iT - 19T^{2}
23 1+8.19T+23T2 1 + 8.19T + 23T^{2}
29 1−3T+29T2 1 - 3T + 29T^{2}
31 1−9.46iT−31T2 1 - 9.46iT - 31T^{2}
37 1+3iT−37T2 1 + 3iT - 37T^{2}
41 1+6.46iT−41T2 1 + 6.46iT - 41T^{2}
43 1−4.19T+43T2 1 - 4.19T + 43T^{2}
47 1+4.73iT−47T2 1 + 4.73iT - 47T^{2}
53 1+3T+53T2 1 + 3T + 53T^{2}
59 1+13.8iT−59T2 1 + 13.8iT - 59T^{2}
61 1−15.1T+61T2 1 - 15.1T + 61T^{2}
67 1−7.26iT−67T2 1 - 7.26iT - 67T^{2}
71 1−2.19iT−71T2 1 - 2.19iT - 71T^{2}
73 1+12.1iT−73T2 1 + 12.1iT - 73T^{2}
79 1−8.39T+79T2 1 - 8.39T + 79T^{2}
83 1+5.66iT−83T2 1 + 5.66iT - 83T^{2}
89 1−9.46iT−89T2 1 - 9.46iT - 89T^{2}
97 1−6iT−97T2 1 - 6iT - 97T^{2}
show more
show less
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−8.528197878448980449414463757416, −8.023083020621778224621612373009, −7.32802233318404623955482718754, −6.51413863725197972569277820583, −5.61531728575718966664116971954, −5.07554022201380351734413285253, −4.11283763399458967427802181847, −3.46794654278528226964588061284, −1.88215650738788830666285664808, −0.76342137354852615322798371255, 0.855595296510717856636467497669, 2.27927250007156010545737945339, 2.88026134974295139236782063997, 3.76992010708974854253397926124, 4.66487284234912939850531083849, 5.71791356953175737763660379785, 6.23219618402024318917055737516, 7.29730763584879703496422085345, 8.023147022633971543702964668515, 8.727927020371192527495451909402

Graph of the ZZ-function along the critical line