↑

Properties

Label 2-3192-3192.293-c0-0-1
Degree $2$
Conductor $3192$
Sign $-0.0977 - 0.995i$
Analytic cond. $1.59301$
Root an. cond. $1.26214$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.5 − 0.866i)2-s + (−0.5 + 0.866i)3-s + (−0.499 − 0.866i)4-s + (1.5 + 0.866i)5-s + (0.499 + 0.866i)6-s − 7-s − 0.999·8-s + (−0.499 − 0.866i)9-s + (1.5 − 0.866i)10-s + 0.999·12-s + (−1.5 + 0.866i)13-s + (−0.5 + 0.866i)14-s + (−1.5 + 0.866i)15-s + (−0.5 + 0.866i)16-s − 0.999·18-s + (−0.5 + 0.866i)19-s + ⋯
L(s)  = 1  + (0.5 − 0.866i)2-s + (−0.5 + 0.866i)3-s + (−0.499 − 0.866i)4-s + (1.5 + 0.866i)5-s + (0.499 + 0.866i)6-s − 7-s − 0.999·8-s + (−0.499 − 0.866i)9-s + (1.5 − 0.866i)10-s + 0.999·12-s + (−1.5 + 0.866i)13-s + (−0.5 + 0.866i)14-s + (−1.5 + 0.866i)15-s + (−0.5 + 0.866i)16-s − 0.999·18-s + (−0.5 + 0.866i)19-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 3192 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.0977 - 0.995i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 3192 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.0977 - 0.995i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(3192\)    =    \(2^{3} \cdot 3 \cdot 7 \cdot 19\)
Sign: $-0.0977 - 0.995i$
Analytic conductor: \(1.59301\)
Root analytic conductor: \(1.26214\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{3192} (293, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 3192,\ (\ :0),\ -0.0977 - 0.995i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.8341476867\)
\(L(\frac12)\) \(\approx\) \(0.8341476867\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (-0.5 + 0.866i)T \)
3 \( 1 + (0.5 - 0.866i)T \)
7 \( 1 + T \)
19 \( 1 + (0.5 - 0.866i)T \)
good5 \( 1 + (-1.5 - 0.866i)T + (0.5 + 0.866i)T^{2} \)
11 \( 1 + T^{2} \)
13 \( 1 + (1.5 - 0.866i)T + (0.5 - 0.866i)T^{2} \)
17 \( 1 + (-0.5 - 0.866i)T^{2} \)
23 \( 1 + (1.5 - 0.866i)T + (0.5 - 0.866i)T^{2} \)
29 \( 1 + (0.5 - 0.866i)T^{2} \)
31 \( 1 + T^{2} \)
37 \( 1 + T^{2} \)
41 \( 1 + (0.5 + 0.866i)T^{2} \)
43 \( 1 + (0.5 + 0.866i)T^{2} \)
47 \( 1 + (-0.5 + 0.866i)T^{2} \)
53 \( 1 + (0.5 - 0.866i)T^{2} \)
59 \( 1 + (0.5 - 0.866i)T + (-0.5 - 0.866i)T^{2} \)
61 \( 1 + (-0.5 - 0.866i)T + (-0.5 + 0.866i)T^{2} \)
67 \( 1 + (-0.5 + 0.866i)T^{2} \)
71 \( 1 + (-0.5 + 0.866i)T + (-0.5 - 0.866i)T^{2} \)
73 \( 1 + (0.5 + 0.866i)T^{2} \)
79 \( 1 + (0.5 + 0.866i)T^{2} \)
83 \( 1 + 1.73iT - T^{2} \)
89 \( 1 + (0.5 - 0.866i)T^{2} \)
97 \( 1 + (-0.5 - 0.866i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

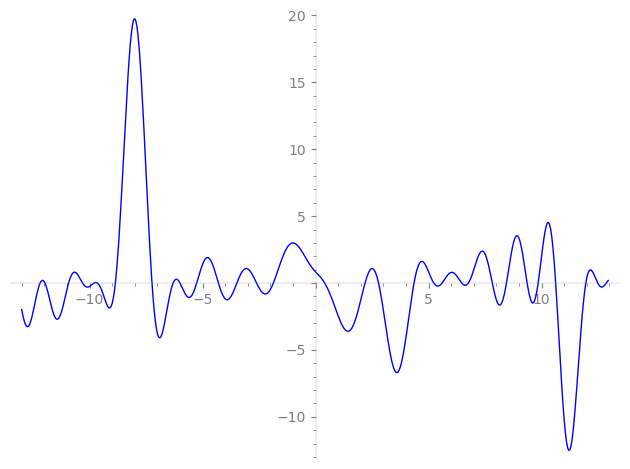
Imaginary part of the first few zeros on the critical line

−9.651761870096336777678852755488, −8.857834216988361040129672692452, −7.23677279832285835682297373041, −6.30232489503217555916736865684, −5.99683365755137734581645831593, −5.25956555204983706503430516854, −4.29747229326049154964493192131, −3.48231288657808892139219937242, −2.61122308010183919382726456172, −1.86709166227319158341888201804, 0.40528198509220683181291794785, 2.18897756105296330703045774770, 2.78687064717018940671356240460, 4.35665576468890754379457018494, 5.23278290290801341763361311744, 5.59672456611350758674225639186, 6.46773586361200729411073917306, 6.76035619515725765372163340007, 7.81999388818909156422510957079, 8.445510600907515858122629948229

Graph of the $Z$-function along the critical line