↑

Properties

Label 2-3248-3248.307-c0-0-0
Degree $2$
Conductor $3248$
Sign $0.979 - 0.201i$
Analytic cond. $1.62096$
Root an. cond. $1.27317$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

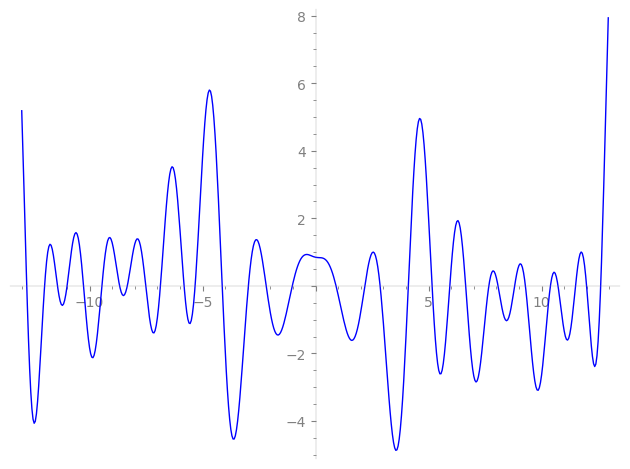
L(s)  = 1  − 2-s + 4-s + 7-s − 8-s − 9-s − 14-s + 16-s + 18-s + i·25-s + 28-s + 29-s − 32-s − 36-s + 2·43-s + 49-s − i·50-s + ⋯
L(s)  = 1  − 2-s + 4-s + 7-s − 8-s − 9-s − 14-s + 16-s + 18-s + i·25-s + 28-s + 29-s − 32-s − 36-s + 2·43-s + 49-s − i·50-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 3248 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.979 - 0.201i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 3248 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.979 - 0.201i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(3248\)    =    \(2^{4} \cdot 7 \cdot 29\)
Sign: $0.979 - 0.201i$
Analytic conductor: \(1.62096\)
Root analytic conductor: \(1.27317\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{3248} (307, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 3248,\ (\ :0),\ 0.979 - 0.201i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.8466814272\)
\(L(\frac12)\) \(\approx\) \(0.8466814272\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + T \)
7 \( 1 - T \)
29 \( 1 - T \)
good3 \( 1 + T^{2} \)
5 \( 1 - iT^{2} \)
11 \( 1 + T^{2} \)
13 \( 1 + iT^{2} \)
17 \( 1 + iT^{2} \)
19 \( 1 + T^{2} \)
23 \( 1 + T^{2} \)
31 \( 1 - iT^{2} \)
37 \( 1 + T^{2} \)
41 \( 1 + iT^{2} \)
43 \( 1 - 2T + T^{2} \)
47 \( 1 + iT^{2} \)
53 \( 1 + (-1 + i)T - iT^{2} \)
59 \( 1 - iT^{2} \)
61 \( 1 - T^{2} \)
67 \( 1 + (-1 - i)T + iT^{2} \)
71 \( 1 - 2iT - T^{2} \)
73 \( 1 + iT^{2} \)
79 \( 1 + (1 + i)T + iT^{2} \)
83 \( 1 + iT^{2} \)
89 \( 1 - iT^{2} \)
97 \( 1 - iT^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−8.669169123759502447910530288252, −8.329973364466046051478228163938, −7.51279116184036266999989923339, −6.86372651829014703807993398501, −5.81616868536283855247807630184, −5.33027175068267797906901932640, −4.13048132632576997271949163170, −2.97326892554484005665052214901, −2.18400660027071355422522475813, −1.02967192569932525265088565312, 0.905411723927944538741942797484, 2.17998584505851809215630760129, 2.85540626242754783418027731214, 4.10313466885390304629178645617, 5.15427182921512863451737905834, 5.93898304515711392371357480592, 6.64153991200497845919031044149, 7.66668530326608183975860618988, 8.072657656966993276945340033109, 8.808022153566740644336177429717

Graph of the $Z$-function along the critical line