↑

Properties

Label 2-3528-7.4-c1-0-45
Degree 22
Conductor 35283528
Sign −0.991+0.126i-0.991 + 0.126i
Analytic cond. 28.171228.1712
Root an. cond. 5.307655.30765
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

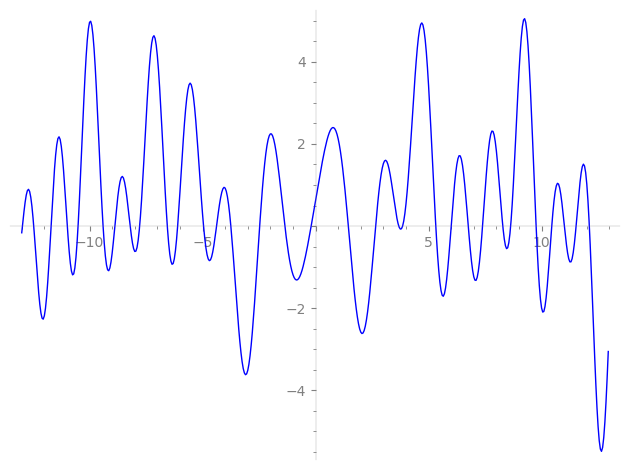
L(s)  = 1  + (−1.41 − 2.44i)5-s + (−1 + 1.73i)11-s + 5.65·13-s + (−1.41 + 2.44i)17-s + (−2.82 − 4.89i)19-s + (−3 − 5.19i)23-s + (−1.49 + 2.59i)25-s − 4·29-s + (2.82 − 4.89i)31-s + (1 + 1.73i)37-s − 2.82·41-s − 4·43-s + (5.65 + 9.79i)47-s + (−6 + 10.3i)53-s + 5.65·55-s + ⋯
L(s)  = 1  + (−0.632 − 1.09i)5-s + (−0.301 + 0.522i)11-s + 1.56·13-s + (−0.342 + 0.594i)17-s + (−0.648 − 1.12i)19-s + (−0.625 − 1.08i)23-s + (−0.299 + 0.519i)25-s − 0.742·29-s + (0.508 − 0.879i)31-s + (0.164 + 0.284i)37-s − 0.441·41-s − 0.609·43-s + (0.825 + 1.42i)47-s + (−0.824 + 1.42i)53-s + 0.762·55-s + ⋯

Functional equation

Λ(s)=(3528s/2 ΓC(s) L(s)=((−0.991+0.126i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 3528 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.991 + 0.126i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(3528s/2 ΓC(s+1/2) L(s)=((−0.991+0.126i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 3528 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.991 + 0.126i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 35283528    =    23⋅32⋅722^{3} \cdot 3^{2} \cdot 7^{2}
Sign: −0.991+0.126i-0.991 + 0.126i
Analytic conductor: 28.171228.1712
Root analytic conductor: 5.307655.30765
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ3528(361,⋅)\chi_{3528} (361, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 3528, ( :1/2), −0.991+0.126i)(2,\ 3528,\ (\ :1/2),\ -0.991 + 0.126i)

Particular Values

L(1)L(1) ≈\approx 0.62798289400.6279828940
L(12)L(\frac12) ≈\approx 0.62798289400.6279828940
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
3 1 1
7 1 1
good5 1+(1.41+2.44i)T+(−2.5+4.33i)T2 1 + (1.41 + 2.44i)T + (-2.5 + 4.33i)T^{2}
11 1+(1−1.73i)T+(−5.5−9.52i)T2 1 + (1 - 1.73i)T + (-5.5 - 9.52i)T^{2}
13 1−5.65T+13T2 1 - 5.65T + 13T^{2}
17 1+(1.41−2.44i)T+(−8.5−14.7i)T2 1 + (1.41 - 2.44i)T + (-8.5 - 14.7i)T^{2}
19 1+(2.82+4.89i)T+(−9.5+16.4i)T2 1 + (2.82 + 4.89i)T + (-9.5 + 16.4i)T^{2}
23 1+(3+5.19i)T+(−11.5+19.9i)T2 1 + (3 + 5.19i)T + (-11.5 + 19.9i)T^{2}
29 1+4T+29T2 1 + 4T + 29T^{2}
31 1+(−2.82+4.89i)T+(−15.5−26.8i)T2 1 + (-2.82 + 4.89i)T + (-15.5 - 26.8i)T^{2}
37 1+(−1−1.73i)T+(−18.5+32.0i)T2 1 + (-1 - 1.73i)T + (-18.5 + 32.0i)T^{2}
41 1+2.82T+41T2 1 + 2.82T + 41T^{2}
43 1+4T+43T2 1 + 4T + 43T^{2}
47 1+(−5.65−9.79i)T+(−23.5+40.7i)T2 1 + (-5.65 - 9.79i)T + (-23.5 + 40.7i)T^{2}
53 1+(6−10.3i)T+(−26.5−45.8i)T2 1 + (6 - 10.3i)T + (-26.5 - 45.8i)T^{2}
59 1+(−5.65+9.79i)T+(−29.5−51.0i)T2 1 + (-5.65 + 9.79i)T + (-29.5 - 51.0i)T^{2}
61 1+(2.82+4.89i)T+(−30.5+52.8i)T2 1 + (2.82 + 4.89i)T + (-30.5 + 52.8i)T^{2}
67 1+(−6+10.3i)T+(−33.5−58.0i)T2 1 + (-6 + 10.3i)T + (-33.5 - 58.0i)T^{2}
71 1+6T+71T2 1 + 6T + 71T^{2}
73 1+(−36.5−63.2i)T2 1 + (-36.5 - 63.2i)T^{2}
79 1+(4+6.92i)T+(−39.5+68.4i)T2 1 + (4 + 6.92i)T + (-39.5 + 68.4i)T^{2}
83 1−11.3T+83T2 1 - 11.3T + 83T^{2}
89 1+(4.24+7.34i)T+(−44.5+77.0i)T2 1 + (4.24 + 7.34i)T + (-44.5 + 77.0i)T^{2}
97 1+11.3T+97T2 1 + 11.3T + 97T^{2}
show more
show less
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−8.201868430388122185112348904984, −7.78333486263716821958233487865, −6.55950255130791717461790073068, −6.10206686275671847625346843454, −4.95553250835819972330296838879, −4.38064270842646198907727175390, −3.74858046341464022964079554106, −2.47274397015080130763037242510, −1.35756320633370239334647848808, −0.19499898755856863083878066500, 1.44915848150364844547056413159, 2.65699591385508786614902251628, 3.68088204535689104773267375777, 3.85111824381347163125414451099, 5.31958347556492921911805582203, 5.99975163820132977448402643375, 6.75582501516725827036933261681, 7.38746469539236020439903240139, 8.284128055691339425415691529969, 8.630803386858349803889810384604

Graph of the ZZ-function along the critical line