↑

Properties

Label 2-3680-115.84-c0-0-1
Degree $2$
Conductor $3680$
Sign $0.808 - 0.588i$
Analytic cond. $1.83655$
Root an. cond. $1.35519$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

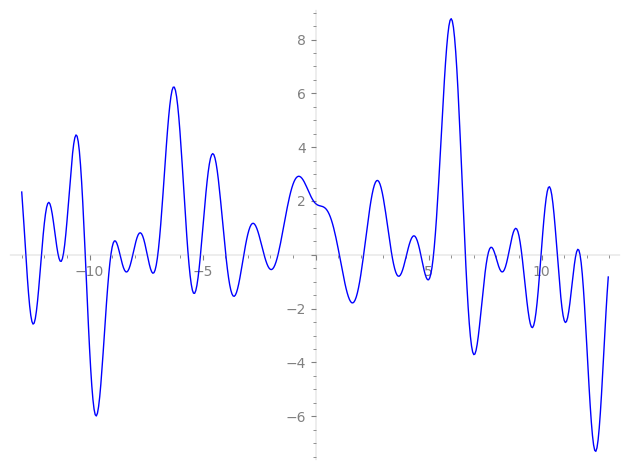
L(s)  = 1  + (1.09 − 0.497i)3-s + (−0.755 + 0.654i)5-s + (1.64 + 1.05i)7-s + (0.285 − 0.329i)9-s + (−0.497 + 1.09i)15-s + (2.31 + 0.333i)21-s + (0.599 + 0.800i)23-s + (0.142 − 0.989i)25-s + (−0.190 + 0.647i)27-s + (−1.25 + 0.368i)29-s + (−1.93 + 0.278i)35-s + (−0.708 − 0.817i)41-s + (−0.729 − 1.59i)43-s + 0.436i·45-s + 0.142i·47-s + ⋯
L(s)  = 1  + (1.09 − 0.497i)3-s + (−0.755 + 0.654i)5-s + (1.64 + 1.05i)7-s + (0.285 − 0.329i)9-s + (−0.497 + 1.09i)15-s + (2.31 + 0.333i)21-s + (0.599 + 0.800i)23-s + (0.142 − 0.989i)25-s + (−0.190 + 0.647i)27-s + (−1.25 + 0.368i)29-s + (−1.93 + 0.278i)35-s + (−0.708 − 0.817i)41-s + (−0.729 − 1.59i)43-s + 0.436i·45-s + 0.142i·47-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 3680 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.808 - 0.588i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 3680 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.808 - 0.588i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(3680\)    =    \(2^{5} \cdot 5 \cdot 23\)
Sign: $0.808 - 0.588i$
Analytic conductor: \(1.83655\)
Root analytic conductor: \(1.35519\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{3680} (3649, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 3680,\ (\ :0),\ 0.808 - 0.588i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.906115632\)
\(L(\frac12)\) \(\approx\) \(1.906115632\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 \)
5 \( 1 + (0.755 - 0.654i)T \)
23 \( 1 + (-0.599 - 0.800i)T \)
good3 \( 1 + (-1.09 + 0.497i)T + (0.654 - 0.755i)T^{2} \)
7 \( 1 + (-1.64 - 1.05i)T + (0.415 + 0.909i)T^{2} \)
11 \( 1 + (0.959 - 0.281i)T^{2} \)
13 \( 1 + (-0.415 + 0.909i)T^{2} \)
17 \( 1 + (0.841 - 0.540i)T^{2} \)
19 \( 1 + (-0.841 - 0.540i)T^{2} \)
29 \( 1 + (1.25 - 0.368i)T + (0.841 - 0.540i)T^{2} \)
31 \( 1 + (-0.654 - 0.755i)T^{2} \)
37 \( 1 + (-0.142 - 0.989i)T^{2} \)
41 \( 1 + (0.708 + 0.817i)T + (-0.142 + 0.989i)T^{2} \)
43 \( 1 + (0.729 + 1.59i)T + (-0.654 + 0.755i)T^{2} \)
47 \( 1 - 0.142iT - T^{2} \)
53 \( 1 + (0.415 + 0.909i)T^{2} \)
59 \( 1 + (0.415 - 0.909i)T^{2} \)
61 \( 1 + (-1.74 - 0.797i)T + (0.654 + 0.755i)T^{2} \)
67 \( 1 + (-0.0994 + 0.691i)T + (-0.959 - 0.281i)T^{2} \)
71 \( 1 + (-0.959 - 0.281i)T^{2} \)
73 \( 1 + (-0.841 - 0.540i)T^{2} \)
79 \( 1 + (-0.415 + 0.909i)T^{2} \)
83 \( 1 + (1.22 - 1.41i)T + (-0.142 - 0.989i)T^{2} \)
89 \( 1 + (-1.80 + 0.822i)T + (0.654 - 0.755i)T^{2} \)
97 \( 1 + (-0.142 + 0.989i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−8.650954471839809099903837315370, −8.086852005555389594001419695601, −7.44592784427851121662415834535, −6.98048495709471603173783506390, −5.63567856610402714854916817719, −5.09143248982754611236212811115, −3.97195211751783610767450591377, −3.17398191815913466890304235639, −2.27681551071833359156465535114, −1.66236203291104878264864555739, 1.05224602767372644078808664114, 2.12630305605077542984929108322, 3.37463734937184264094208059405, 4.02743116300192030575928637650, 4.65590458789864105735356932556, 5.21878626311066504081244890958, 6.62661397917501052559172023170, 7.62194398943483377381729460108, 7.947537552807281787971267507959, 8.529505867260315527596468832973

Graph of the $Z$-function along the critical line