↑

Properties

Label 2-3960-1320.1139-c0-0-4
Degree $2$
Conductor $3960$
Sign $0.422 - 0.906i$
Analytic cond. $1.97629$
Root an. cond. $1.40580$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.309 + 0.951i)2-s + (−0.809 + 0.587i)4-s + (0.951 + 0.309i)5-s + (−1.16 − 1.59i)7-s + (−0.809 − 0.587i)8-s + 0.999i·10-s + (−0.156 + 0.987i)11-s + (0.863 − 0.280i)13-s + (1.16 − 1.59i)14-s + (0.309 − 0.951i)16-s + (0.363 − 0.5i)19-s + (−0.951 + 0.309i)20-s + (−0.987 + 0.156i)22-s + 1.61i·23-s + (0.809 + 0.587i)25-s + (0.533 + 0.734i)26-s + ⋯
L(s)  = 1  + (0.309 + 0.951i)2-s + (−0.809 + 0.587i)4-s + (0.951 + 0.309i)5-s + (−1.16 − 1.59i)7-s + (−0.809 − 0.587i)8-s + 0.999i·10-s + (−0.156 + 0.987i)11-s + (0.863 − 0.280i)13-s + (1.16 − 1.59i)14-s + (0.309 − 0.951i)16-s + (0.363 − 0.5i)19-s + (−0.951 + 0.309i)20-s + (−0.987 + 0.156i)22-s + 1.61i·23-s + (0.809 + 0.587i)25-s + (0.533 + 0.734i)26-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 3960 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.422 - 0.906i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 3960 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.422 - 0.906i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(3960\)    =    \(2^{3} \cdot 3^{2} \cdot 5 \cdot 11\)
Sign: $0.422 - 0.906i$
Analytic conductor: \(1.97629\)
Root analytic conductor: \(1.40580\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{3960} (3779, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 3960,\ (\ :0),\ 0.422 - 0.906i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.481799063\)
\(L(\frac12)\) \(\approx\) \(1.481799063\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (-0.309 - 0.951i)T \)
3 \( 1 \)
5 \( 1 + (-0.951 - 0.309i)T \)
11 \( 1 + (0.156 - 0.987i)T \)
good7 \( 1 + (1.16 + 1.59i)T + (-0.309 + 0.951i)T^{2} \)
13 \( 1 + (-0.863 + 0.280i)T + (0.809 - 0.587i)T^{2} \)
17 \( 1 + (0.809 + 0.587i)T^{2} \)
19 \( 1 + (-0.363 + 0.5i)T + (-0.309 - 0.951i)T^{2} \)
23 \( 1 - 1.61iT - T^{2} \)
29 \( 1 + (-0.309 + 0.951i)T^{2} \)
31 \( 1 + (0.809 - 0.587i)T^{2} \)
37 \( 1 + (-1.44 + 1.04i)T + (0.309 - 0.951i)T^{2} \)
41 \( 1 + (-0.253 - 0.183i)T + (0.309 + 0.951i)T^{2} \)
43 \( 1 + T^{2} \)
47 \( 1 + (-1.11 + 1.53i)T + (-0.309 - 0.951i)T^{2} \)
53 \( 1 + (-1.11 + 0.363i)T + (0.809 - 0.587i)T^{2} \)
59 \( 1 + (-1.04 - 1.44i)T + (-0.309 + 0.951i)T^{2} \)
61 \( 1 + (-0.809 - 0.587i)T^{2} \)
67 \( 1 - T^{2} \)
71 \( 1 + (-0.809 - 0.587i)T^{2} \)
73 \( 1 + (0.309 - 0.951i)T^{2} \)
79 \( 1 + (-0.809 + 0.587i)T^{2} \)
83 \( 1 + (0.809 + 0.587i)T^{2} \)
89 \( 1 + 0.312iT - T^{2} \)
97 \( 1 + (0.809 - 0.587i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

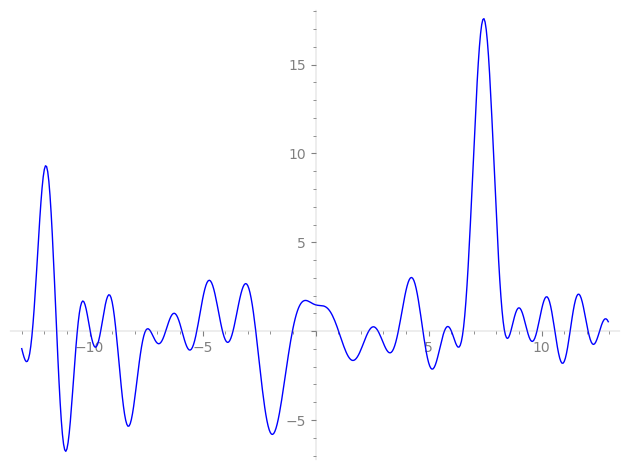
Imaginary part of the first few zeros on the critical line

−8.828339766243672067784300892253, −7.52973112452388742617903196878, −7.30333206183258453680634021742, −6.63148328503522691658231682721, −5.90917716695953143924542274681, −5.25623953817212222934631272855, −4.11705539995037436833043978138, −3.65365548105367691424483610897, −2.64522871970484653334397824677, −1.02397938545570086339597966092, 1.01855643797560794593288604239, 2.35030793761958260666208541378, 2.76661879373709806735809045412, 3.66057438486672440453985772199, 4.75169852463133925319726706989, 5.69802617454890655040955431756, 6.00916308767809429198804498962, 6.52688327775229899459714285694, 8.361599873605852928913109014502, 8.638992913954445298202071406176

Graph of the $Z$-function along the critical line