↑

Properties

Label 2-399-7.4-c1-0-19
Degree 22
Conductor 399399
Sign −0.0857−0.996i-0.0857 - 0.996i
Analytic cond. 3.186033.18603
Root an. cond. 1.784941.78494
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−1.28 − 2.23i)2-s + (−0.5 + 0.866i)3-s + (−2.32 + 4.02i)4-s + (−1.82 − 3.15i)5-s + 2.57·6-s + (0.967 − 2.46i)7-s + 6.80·8-s + (−0.499 − 0.866i)9-s + (−4.69 + 8.12i)10-s + (2.06 − 3.58i)11-s + (−2.32 − 4.02i)12-s − 4.13·13-s + (−6.74 + 1.01i)14-s + 3.64·15-s + (−4.13 − 7.15i)16-s + (−1.5 + 2.59i)17-s + ⋯
L(s)  = 1  + (−0.911 − 1.57i)2-s + (−0.288 + 0.499i)3-s + (−1.16 + 2.01i)4-s + (−0.814 − 1.41i)5-s + 1.05·6-s + (0.365 − 0.930i)7-s + 2.40·8-s + (−0.166 − 0.288i)9-s + (−1.48 + 2.57i)10-s + (0.623 − 1.08i)11-s + (−0.670 − 1.16i)12-s − 1.14·13-s + (−1.80 + 0.270i)14-s + 0.940·15-s + (−1.03 − 1.78i)16-s + (−0.363 + 0.630i)17-s + ⋯

Functional equation

Λ(s)=(399s/2 ΓC(s) L(s)=((−0.0857−0.996i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 399 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.0857 - 0.996i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(399s/2 ΓC(s+1/2) L(s)=((−0.0857−0.996i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 399 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.0857 - 0.996i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 399399    =    3⋅7⋅193 \cdot 7 \cdot 19
Sign: −0.0857−0.996i-0.0857 - 0.996i
Analytic conductor: 3.186033.18603
Root analytic conductor: 1.784941.78494
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ399(172,⋅)\chi_{399} (172, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 399, ( :1/2), −0.0857−0.996i)(2,\ 399,\ (\ :1/2),\ -0.0857 - 0.996i)

Particular Values

L(1)L(1) ≈\approx 0.172963+0.188491i0.172963 + 0.188491i
L(12)L(\frac12) ≈\approx 0.172963+0.188491i0.172963 + 0.188491i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad3 1+(0.5−0.866i)T 1 + (0.5 - 0.866i)T
7 1+(−0.967+2.46i)T 1 + (-0.967 + 2.46i)T
19 1+(−0.5−0.866i)T 1 + (-0.5 - 0.866i)T
good2 1+(1.28+2.23i)T+(−1+1.73i)T2 1 + (1.28 + 2.23i)T + (-1 + 1.73i)T^{2}
5 1+(1.82+3.15i)T+(−2.5+4.33i)T2 1 + (1.82 + 3.15i)T + (-2.5 + 4.33i)T^{2}
11 1+(−2.06+3.58i)T+(−5.5−9.52i)T2 1 + (-2.06 + 3.58i)T + (-5.5 - 9.52i)T^{2}
13 1+4.13T+13T2 1 + 4.13T + 13T^{2}
17 1+(1.5−2.59i)T+(−8.5−14.7i)T2 1 + (1.5 - 2.59i)T + (-8.5 - 14.7i)T^{2}
23 1+(−1.41−2.45i)T+(−11.5+19.9i)T2 1 + (-1.41 - 2.45i)T + (-11.5 + 19.9i)T^{2}
29 1+8.66T+29T2 1 + 8.66T + 29T^{2}
31 1+(4.14−7.18i)T+(−15.5−26.8i)T2 1 + (4.14 - 7.18i)T + (-15.5 - 26.8i)T^{2}
37 1+(−0.172−0.298i)T+(−18.5+32.0i)T2 1 + (-0.172 - 0.298i)T + (-18.5 + 32.0i)T^{2}
41 1−3.31T+41T2 1 - 3.31T + 41T^{2}
43 1−6.00T+43T2 1 - 6.00T + 43T^{2}
47 1+(4.35+7.54i)T+(−23.5+40.7i)T2 1 + (4.35 + 7.54i)T + (-23.5 + 40.7i)T^{2}
53 1+(−2.50+4.34i)T+(−26.5−45.8i)T2 1 + (-2.50 + 4.34i)T + (-26.5 - 45.8i)T^{2}
59 1+(3.00−5.20i)T+(−29.5−51.0i)T2 1 + (3.00 - 5.20i)T + (-29.5 - 51.0i)T^{2}
61 1+(−0.181−0.314i)T+(−30.5+52.8i)T2 1 + (-0.181 - 0.314i)T + (-30.5 + 52.8i)T^{2}
67 1+(−4.24+7.35i)T+(−33.5−58.0i)T2 1 + (-4.24 + 7.35i)T + (-33.5 - 58.0i)T^{2}
71 1+5.88T+71T2 1 + 5.88T + 71T^{2}
73 1+(−5.50+9.53i)T+(−36.5−63.2i)T2 1 + (-5.50 + 9.53i)T + (-36.5 - 63.2i)T^{2}
79 1+(−5.39−9.33i)T+(−39.5+68.4i)T2 1 + (-5.39 - 9.33i)T + (-39.5 + 68.4i)T^{2}
83 1+17.3T+83T2 1 + 17.3T + 83T^{2}
89 1+(−5.32−9.22i)T+(−44.5+77.0i)T2 1 + (-5.32 - 9.22i)T + (-44.5 + 77.0i)T^{2}
97 1−1.21T+97T2 1 - 1.21T + 97T^{2}
show more
show less
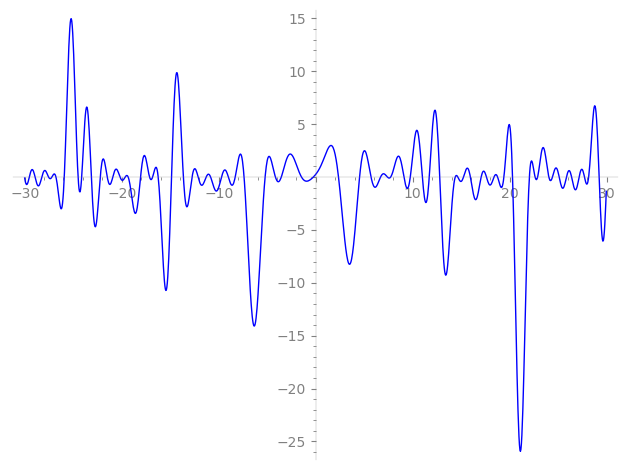
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.83456397989575727558500373540, −9.712609092269909008395188070745, −9.005030736297470786050633881496, −8.301361180689588999399025096679, −7.38666349674295633350250507246, −5.21730333383282753861490840072, −4.15347758796463648473387294337, −3.55006981708457487248284724051, −1.46495551932363390506282059762, −0.24717407924063765583436559115, 2.34797165912495807673112095096, 4.52037087101876579045664366386, 5.70165795762043367771054835620, 6.68318842251652829665337800431, 7.39039340241357597664387242651, 7.72159554481953050398378171148, 9.095682162857757446499945788915, 9.746792465279353292941149241943, 10.99294561282799894868369121046, 11.70004107320202285065648597597

Graph of the ZZ-function along the critical line