↑

Properties

Label 2-4000-5.4-c1-0-29
Degree 22
Conductor 40004000
Sign −i-i
Analytic cond. 31.940131.9401
Root an. cond. 5.651565.65156
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 0.902i·3-s + 0.891i·7-s + 2.18·9-s − 0.804·21-s + 3.04i·23-s + 4.67i·27-s + 0.403·29-s + 3.43·41-s − 1.13i·43-s + 7.82i·47-s + 6.20·49-s − 3.46·61-s + 1.94i·63-s + 14.1i·67-s − 2.74·69-s + ⋯
L(s)  = 1  + 0.520i·3-s + 0.336i·7-s + 0.728·9-s − 0.175·21-s + 0.635i·23-s + 0.900i·27-s + 0.0748·29-s + 0.536·41-s − 0.172i·43-s + 1.14i·47-s + 0.886·49-s − 0.443·61-s + 0.245i·63-s + 1.73i·67-s − 0.330·69-s + ⋯

Functional equation

Λ(s)=(4000s/2 ΓC(s) L(s)=(−i Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 4000 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -i\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(4000s/2 ΓC(s+1/2) L(s)=(−i Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 4000 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & -i\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 40004000    =    25⋅532^{5} \cdot 5^{3}
Sign: −i-i
Analytic conductor: 31.940131.9401
Root analytic conductor: 5.651565.65156
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ4000(1249,⋅)\chi_{4000} (1249, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 4000, ( :1/2), −i)(2,\ 4000,\ (\ :1/2),\ -i)

Particular Values

L(1)L(1) ≈\approx 1.8619705521.861970552
L(12)L(\frac12) ≈\approx 1.8619705521.861970552
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
5 1 1
good3 1−0.902iT−3T2 1 - 0.902iT - 3T^{2}
7 1−0.891iT−7T2 1 - 0.891iT - 7T^{2}
11 1+11T2 1 + 11T^{2}
13 1−13T2 1 - 13T^{2}
17 1−17T2 1 - 17T^{2}
19 1+19T2 1 + 19T^{2}
23 1−3.04iT−23T2 1 - 3.04iT - 23T^{2}
29 1−0.403T+29T2 1 - 0.403T + 29T^{2}
31 1+31T2 1 + 31T^{2}
37 1−37T2 1 - 37T^{2}
41 1−3.43T+41T2 1 - 3.43T + 41T^{2}
43 1+1.13iT−43T2 1 + 1.13iT - 43T^{2}
47 1−7.82iT−47T2 1 - 7.82iT - 47T^{2}
53 1−53T2 1 - 53T^{2}
59 1+59T2 1 + 59T^{2}
61 1+3.46T+61T2 1 + 3.46T + 61T^{2}
67 1−14.1iT−67T2 1 - 14.1iT - 67T^{2}
71 1+71T2 1 + 71T^{2}
73 1−73T2 1 - 73T^{2}
79 1+79T2 1 + 79T^{2}
83 1+15.5iT−83T2 1 + 15.5iT - 83T^{2}
89 1−15.1T+89T2 1 - 15.1T + 89T^{2}
97 1−97T2 1 - 97T^{2}
show more
show less
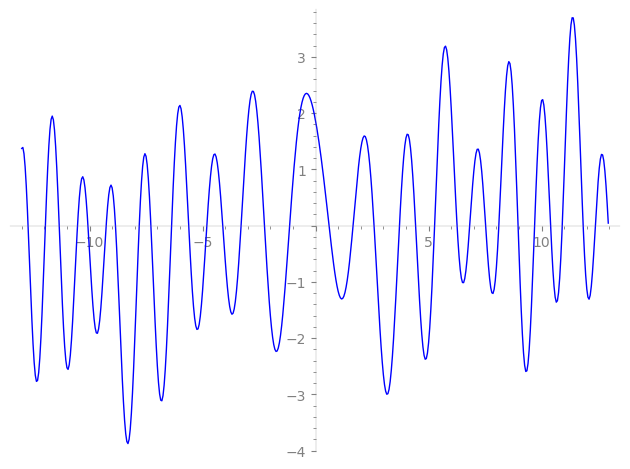
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−8.852758292964859763322004803591, −7.80113892279838245315834132499, −7.28556713563846482876308679909, −6.37141466160232890514301735484, −5.61231085621493620541464017919, −4.81119127184203426336565773232, −4.10636613340677726041354376455, −3.29539306889793677538660948188, −2.26009220005354461782973869696, −1.14849613316856553100799179305, 0.59680998547117400906819491012, 1.65832261930083873131831508860, 2.58780830653611020963398655993, 3.71170451602661189269095506454, 4.42663380413081121310575497751, 5.26628954529932169917760323345, 6.26057996463337849094535932507, 6.81877938092145426542807913199, 7.52403535103178599802949645954, 8.108231474387351440122375336780

Graph of the ZZ-function along the critical line