↑

Properties

Label 2-21e2-63.25-c1-0-6
Degree $2$
Conductor $441$
Sign $-0.154 - 0.987i$
Analytic cond. $3.52140$
Root an. cond. $1.87654$
Motivic weight $1$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 1.69·2-s + (0.175 + 1.72i)3-s + 0.888·4-s + (0.474 − 0.822i)5-s + (−0.298 − 2.92i)6-s + 1.88·8-s + (−2.93 + 0.605i)9-s + (−0.806 + 1.39i)10-s + (0.294 + 0.509i)11-s + (0.156 + 1.53i)12-s + (2.50 + 4.34i)13-s + (1.5 + 0.673i)15-s − 4.98·16-s + (3.79 − 6.56i)17-s + (4.99 − 1.02i)18-s + (2.23 + 3.86i)19-s + ⋯
L(s)  = 1  − 1.20·2-s + (0.101 + 0.994i)3-s + 0.444·4-s + (0.212 − 0.367i)5-s + (−0.121 − 1.19i)6-s + 0.667·8-s + (−0.979 + 0.201i)9-s + (−0.255 + 0.441i)10-s + (0.0886 + 0.153i)11-s + (0.0451 + 0.442i)12-s + (0.696 + 1.20i)13-s + (0.387 + 0.173i)15-s − 1.24·16-s + (0.919 − 1.59i)17-s + (1.17 − 0.242i)18-s + (0.511 + 0.886i)19-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 441 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.154 - 0.987i)\, \overline{\Lambda}(2-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 441 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.154 - 0.987i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(441\)    =    \(3^{2} \cdot 7^{2}\)
Sign: $-0.154 - 0.987i$
Analytic conductor: \(3.52140\)
Root analytic conductor: \(1.87654\)
Motivic weight: \(1\)
Rational: no
Arithmetic: yes
Character: $\chi_{441} (214, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 441,\ (\ :1/2),\ -0.154 - 0.987i)\)

Particular Values

\(L(1)\) \(\approx\) \(0.458210 + 0.535682i\)
\(L(\frac12)\) \(\approx\) \(0.458210 + 0.535682i\)
\(L(\frac{3}{2})\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad3 \( 1 + (-0.175 - 1.72i)T \)
7 \( 1 \)
good2 \( 1 + 1.69T + 2T^{2} \)
5 \( 1 + (-0.474 + 0.822i)T + (-2.5 - 4.33i)T^{2} \)
11 \( 1 + (-0.294 - 0.509i)T + (-5.5 + 9.52i)T^{2} \)
13 \( 1 + (-2.50 - 4.34i)T + (-6.5 + 11.2i)T^{2} \)
17 \( 1 + (-3.79 + 6.56i)T + (-8.5 - 14.7i)T^{2} \)
19 \( 1 + (-2.23 - 3.86i)T + (-9.5 + 16.4i)T^{2} \)
23 \( 1 + (1.23 - 2.14i)T + (-11.5 - 19.9i)T^{2} \)
29 \( 1 + (2.73 - 4.74i)T + (-14.5 - 25.1i)T^{2} \)
31 \( 1 + 6.07T + 31T^{2} \)
37 \( 1 + (-3.49 - 6.05i)T + (-18.5 + 32.0i)T^{2} \)
41 \( 1 + (-0.527 - 0.913i)T + (-20.5 + 35.5i)T^{2} \)
43 \( 1 + (3.49 - 6.05i)T + (-21.5 - 37.2i)T^{2} \)
47 \( 1 + 7.47T + 47T^{2} \)
53 \( 1 + (3.46 - 5.99i)T + (-26.5 - 45.8i)T^{2} \)
59 \( 1 - 10.4T + 59T^{2} \)
61 \( 1 - 11.6T + 61T^{2} \)
67 \( 1 + 11.8T + 67T^{2} \)
71 \( 1 - 4.30T + 71T^{2} \)
73 \( 1 + (2.23 - 3.86i)T + (-36.5 - 63.2i)T^{2} \)
79 \( 1 + 1.33T + 79T^{2} \)
83 \( 1 + (-2.84 + 4.92i)T + (-41.5 - 71.8i)T^{2} \)
89 \( 1 + (0.421 + 0.730i)T + (-44.5 + 77.0i)T^{2} \)
97 \( 1 + (-1.70 + 2.94i)T + (-48.5 - 84.0i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

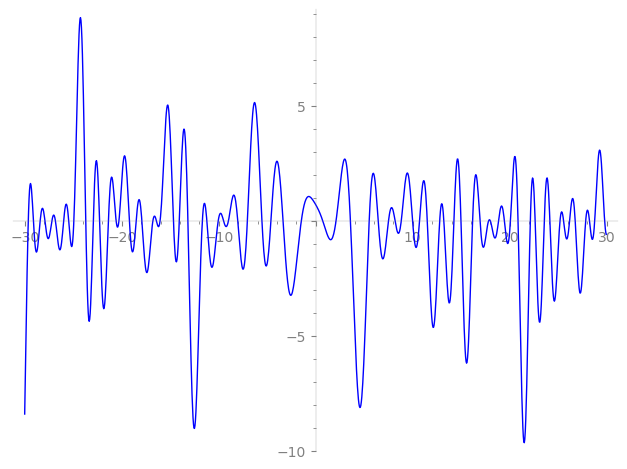
Imaginary part of the first few zeros on the critical line

−11.22116197663704349037386080188, −10.05128031632673280274990252485, −9.499756555602935691705799805779, −8.998856828782080792625965019814, −8.037284899142455764759125072043, −7.04598163848948017495439506938, −5.54450183014960597903742450518, −4.61819611761172619370292157909, −3.37034421877396565540693327987, −1.48517922615807702866077263518, 0.72318971294014726046419862601, 2.09330994365511835033269380961, 3.57571208621274936039268884031, 5.51110293983403985803222925369, 6.44118221603083359049984824188, 7.50169149488329629351164359801, 8.182712498916013788561657975683, 8.817253749687301389657331984886, 9.985450854574256241010860144722, 10.70049880153713799999447312897

Graph of the $Z$-function along the critical line