↑

Properties

Label 2-450-5.4-c3-0-1
Degree 22
Conductor 450450
Sign −0.447+0.894i-0.447 + 0.894i
Analytic cond. 26.550826.5508
Root an. cond. 5.152755.15275
Motivic weight 33
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 2i·2-s − 4·4-s + 34i·7-s − 8i·8-s − 27·11-s − 28i·13-s − 68·14-s + 16·16-s + 21i·17-s − 35·19-s − 54i·22-s + 78i·23-s + 56·26-s − 136i·28-s − 120·29-s + ⋯
L(s)  = 1  + 0.707i·2-s − 0.5·4-s + 1.83i·7-s − 0.353i·8-s − 0.740·11-s − 0.597i·13-s − 1.29·14-s + 0.250·16-s + 0.299i·17-s − 0.422·19-s − 0.523i·22-s + 0.707i·23-s + 0.422·26-s − 0.917i·28-s − 0.768·29-s + ⋯

Functional equation

Λ(s)=(450s/2 ΓC(s) L(s)=((−0.447+0.894i) Λ‾(4−s)\begin{aligned}\Lambda(s)=\mathstrut & 450 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.447 + 0.894i)\, \overline{\Lambda}(4-s) \end{aligned}
Λ(s)=(450s/2 ΓC(s+3/2) L(s)=((−0.447+0.894i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 450 ^{s/2} \, \Gamma_{\C}(s+3/2) \, L(s)\cr =\mathstrut & (-0.447 + 0.894i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 450450    =    2⋅32⋅522 \cdot 3^{2} \cdot 5^{2}
Sign: −0.447+0.894i-0.447 + 0.894i
Analytic conductor: 26.550826.5508
Root analytic conductor: 5.152755.15275
Motivic weight: 33
Rational: no
Arithmetic: yes
Character: χ450(199,⋅)\chi_{450} (199, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 450, ( :3/2), −0.447+0.894i)(2,\ 450,\ (\ :3/2),\ -0.447 + 0.894i)

Particular Values

L(2)L(2) ≈\approx 0.34258826910.3425882691
L(12)L(\frac12) ≈\approx 0.34258826910.3425882691
L(52)L(\frac{5}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1−2iT 1 - 2iT
3 1 1
5 1 1
good7 1−34iT−343T2 1 - 34iT - 343T^{2}
11 1+27T+1.33e3T2 1 + 27T + 1.33e3T^{2}
13 1+28iT−2.19e3T2 1 + 28iT - 2.19e3T^{2}
17 1−21iT−4.91e3T2 1 - 21iT - 4.91e3T^{2}
19 1+35T+6.85e3T2 1 + 35T + 6.85e3T^{2}
23 1−78iT−1.21e4T2 1 - 78iT - 1.21e4T^{2}
29 1+120T+2.43e4T2 1 + 120T + 2.43e4T^{2}
31 1−182T+2.97e4T2 1 - 182T + 2.97e4T^{2}
37 1+146iT−5.06e4T2 1 + 146iT - 5.06e4T^{2}
41 1+357T+6.89e4T2 1 + 357T + 6.89e4T^{2}
43 1+148iT−7.95e4T2 1 + 148iT - 7.95e4T^{2}
47 1+84iT−1.03e5T2 1 + 84iT - 1.03e5T^{2}
53 1+702iT−1.48e5T2 1 + 702iT - 1.48e5T^{2}
59 1+840T+2.05e5T2 1 + 840T + 2.05e5T^{2}
61 1+238T+2.26e5T2 1 + 238T + 2.26e5T^{2}
67 1+461iT−3.00e5T2 1 + 461iT - 3.00e5T^{2}
71 1−708T+3.57e5T2 1 - 708T + 3.57e5T^{2}
73 1+133iT−3.89e5T2 1 + 133iT - 3.89e5T^{2}
79 1+650T+4.93e5T2 1 + 650T + 4.93e5T^{2}
83 1−903iT−5.71e5T2 1 - 903iT - 5.71e5T^{2}
89 1−735T+7.04e5T2 1 - 735T + 7.04e5T^{2}
97 1+1.10e3iT−9.12e5T2 1 + 1.10e3iT - 9.12e5T^{2}
show more
show less
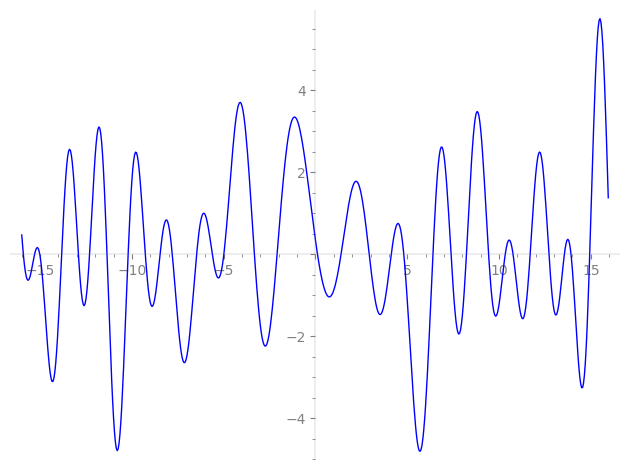
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.35568638200711736463865723103, −10.20386161817641087865381003514, −9.268240080196071559951718991828, −8.463509399496716743683138674638, −7.80019920591031056105901603379, −6.47252091606453736172641999980, −5.61630957668637738770397233042, −4.99029791363619424145833822362, −3.32552159689396697349887064991, −2.09063581339734631606879067464, 0.11070624202348647325579644946, 1.39375735391236763612693226048, 2.92843645948722397101641318163, 4.13000755981286065308972713479, 4.81157660181719653220600379830, 6.39927166337522203123580360053, 7.38667708460933914260209778934, 8.224290522001209330590792524291, 9.431014774144783312555474101921, 10.33780407002663614960805793318

Graph of the ZZ-function along the critical line