↑

Properties

Label 2-450-5.2-c6-0-28
Degree 22
Conductor 450450
Sign −0.229−0.973i-0.229 - 0.973i
Analytic cond. 103.524103.524
Root an. cond. 10.174610.1746
Motivic weight 66
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (4 + 4i)2-s + 32i·4-s + (362. + 362. i)7-s + (−128 + 128i)8-s + 1.32e3·11-s + (−254. + 254. i)13-s + 2.90e3i·14-s − 1.02e3·16-s + (4.39e3 + 4.39e3i)17-s − 819. i·19-s + (5.28e3 + 5.28e3i)22-s + (1.11e4 − 1.11e4i)23-s − 2.03e3·26-s + (−1.16e4 + 1.16e4i)28-s + 2.74e4i·29-s + ⋯
L(s)  = 1  + (0.5 + 0.5i)2-s + 0.5i·4-s + (1.05 + 1.05i)7-s + (−0.250 + 0.250i)8-s + 0.992·11-s + (−0.115 + 0.115i)13-s + 1.05i·14-s − 0.250·16-s + (0.895 + 0.895i)17-s − 0.119i·19-s + (0.496 + 0.496i)22-s + (0.915 − 0.915i)23-s − 0.115·26-s + (−0.528 + 0.528i)28-s + 1.12i·29-s + ⋯

Functional equation

Λ(s)=(450s/2 ΓC(s) L(s)=((−0.229−0.973i) Λ‾(7−s)\begin{aligned}\Lambda(s)=\mathstrut & 450 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.229 - 0.973i)\, \overline{\Lambda}(7-s) \end{aligned}
Λ(s)=(450s/2 ΓC(s+3) L(s)=((−0.229−0.973i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 450 ^{s/2} \, \Gamma_{\C}(s+3) \, L(s)\cr =\mathstrut & (-0.229 - 0.973i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 450450    =    2⋅32⋅522 \cdot 3^{2} \cdot 5^{2}
Sign: −0.229−0.973i-0.229 - 0.973i
Analytic conductor: 103.524103.524
Root analytic conductor: 10.174610.1746
Motivic weight: 66
Rational: no
Arithmetic: yes
Character: χ450(307,⋅)\chi_{450} (307, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 450, ( :3), −0.229−0.973i)(2,\ 450,\ (\ :3),\ -0.229 - 0.973i)

Particular Values

L(72)L(\frac{7}{2}) ≈\approx 3.9017081813.901708181
L(12)L(\frac12) ≈\approx 3.9017081813.901708181
L(4)L(4) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(−4−4i)T 1 + (-4 - 4i)T
3 1 1
5 1 1
good7 1+(−362.−362.i)T+1.17e5iT2 1 + (-362. - 362. i)T + 1.17e5iT^{2}
11 1−1.32e3T+1.77e6T2 1 - 1.32e3T + 1.77e6T^{2}
13 1+(254.−254.i)T−4.82e6iT2 1 + (254. - 254. i)T - 4.82e6iT^{2}
17 1+(−4.39e3−4.39e3i)T+2.41e7iT2 1 + (-4.39e3 - 4.39e3i)T + 2.41e7iT^{2}
19 1+819.iT−4.70e7T2 1 + 819. iT - 4.70e7T^{2}
23 1+(−1.11e4+1.11e4i)T−1.48e8iT2 1 + (-1.11e4 + 1.11e4i)T - 1.48e8iT^{2}
29 1−2.74e4iT−5.94e8T2 1 - 2.74e4iT - 5.94e8T^{2}
31 1−1.50e4T+8.87e8T2 1 - 1.50e4T + 8.87e8T^{2}
37 1+(2.15e4+2.15e4i)T+2.56e9iT2 1 + (2.15e4 + 2.15e4i)T + 2.56e9iT^{2}
41 1−4.56e4T+4.75e9T2 1 - 4.56e4T + 4.75e9T^{2}
43 1+(−7.81e4+7.81e4i)T−6.32e9iT2 1 + (-7.81e4 + 7.81e4i)T - 6.32e9iT^{2}
47 1+(1.99e3+1.99e3i)T+1.07e10iT2 1 + (1.99e3 + 1.99e3i)T + 1.07e10iT^{2}
53 1+(−1.06e5+1.06e5i)T−2.21e10iT2 1 + (-1.06e5 + 1.06e5i)T - 2.21e10iT^{2}
59 1+6.44e4iT−4.21e10T2 1 + 6.44e4iT - 4.21e10T^{2}
61 1+3.20e5T+5.15e10T2 1 + 3.20e5T + 5.15e10T^{2}
67 1+(−3.50e4−3.50e4i)T+9.04e10iT2 1 + (-3.50e4 - 3.50e4i)T + 9.04e10iT^{2}
71 1−2.51e5T+1.28e11T2 1 - 2.51e5T + 1.28e11T^{2}
73 1+(3.26e5−3.26e5i)T−1.51e11iT2 1 + (3.26e5 - 3.26e5i)T - 1.51e11iT^{2}
79 1+2.57e4iT−2.43e11T2 1 + 2.57e4iT - 2.43e11T^{2}
83 1+(1.23e5−1.23e5i)T−3.26e11iT2 1 + (1.23e5 - 1.23e5i)T - 3.26e11iT^{2}
89 1+1.98e5iT−4.96e11T2 1 + 1.98e5iT - 4.96e11T^{2}
97 1+(−7.38e5−7.38e5i)T+8.32e11iT2 1 + (-7.38e5 - 7.38e5i)T + 8.32e11iT^{2}
show more
show less
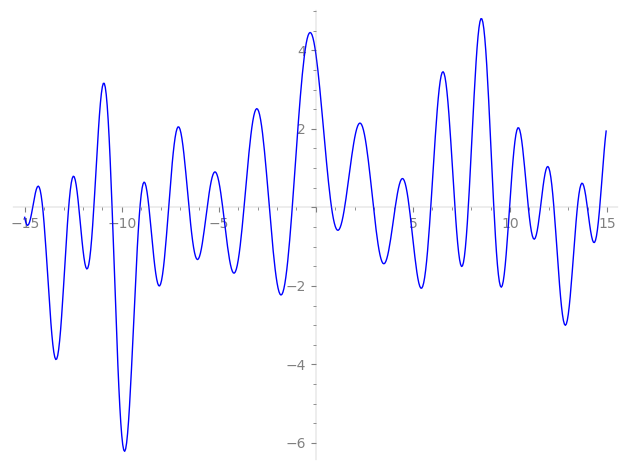
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.49899875136955644813774903029, −9.063149947254500167899701137658, −8.599920332186315433056078815896, −7.58394142126644643908830394758, −6.53669355065361700236131997863, −5.60041231498892687565561022108, −4.80049265550793102491263147102, −3.70252776374047082903246899760, −2.39743120110000453659291709781, −1.21797566751184326770236933387, 0.804183475403028501775609627457, 1.47940989412192124501967383082, 2.96700992366751523280767277000, 4.08475045999109777530163188242, 4.80804246813951560590907938710, 5.91570995710097906281908362720, 7.16195738301155980816298033170, 7.84948522454693229051838798935, 9.164415648449143602480766607887, 9.974790004982237691257584688752

Graph of the ZZ-function along the critical line