↑

Properties

Label 2-538-269.187-c2-0-30
Degree 22
Conductor 538538
Sign 0.157+0.987i0.157 + 0.987i
Analytic cond. 14.659414.6594
Root an. cond. 3.828763.82876
Motivic weight 22
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (1 + i)2-s + (0.991 + 0.991i)3-s + 2i·4-s − 6.41·5-s + 1.98i·6-s + (−6.33 + 6.33i)7-s + (−2 + 2i)8-s − 7.03i·9-s + (−6.41 − 6.41i)10-s + 6.36i·11-s + (−1.98 + 1.98i)12-s − 22.5i·13-s − 12.6·14-s + (−6.35 − 6.35i)15-s − 4·16-s + (−1.76 − 1.76i)17-s + ⋯
L(s)  = 1  + (0.5 + 0.5i)2-s + (0.330 + 0.330i)3-s + 0.5i·4-s − 1.28·5-s + 0.330i·6-s + (−0.904 + 0.904i)7-s + (−0.250 + 0.250i)8-s − 0.781i·9-s + (−0.641 − 0.641i)10-s + 0.578i·11-s + (−0.165 + 0.165i)12-s − 1.73i·13-s − 0.904·14-s + (−0.423 − 0.423i)15-s − 0.250·16-s + (−0.103 − 0.103i)17-s + ⋯

Functional equation

Λ(s)=(538s/2 ΓC(s) L(s)=((0.157+0.987i) Λ‾(3−s)\begin{aligned}\Lambda(s)=\mathstrut & 538 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.157 + 0.987i)\, \overline{\Lambda}(3-s) \end{aligned}
Λ(s)=(538s/2 ΓC(s+1) L(s)=((0.157+0.987i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 538 ^{s/2} \, \Gamma_{\C}(s+1) \, L(s)\cr =\mathstrut & (0.157 + 0.987i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 538538    =    2⋅2692 \cdot 269
Sign: 0.157+0.987i0.157 + 0.987i
Analytic conductor: 14.659414.6594
Root analytic conductor: 3.828763.82876
Motivic weight: 22
Rational: no
Arithmetic: yes
Character: χ538(187,⋅)\chi_{538} (187, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 538, ( :1), 0.157+0.987i)(2,\ 538,\ (\ :1),\ 0.157 + 0.987i)

Particular Values

L(32)L(\frac{3}{2}) ≈\approx 0.57794815140.5779481514
L(12)L(\frac12) ≈\approx 0.57794815140.5779481514
L(2)L(2) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(−1−i)T 1 + (-1 - i)T
269 1+(219.−155.i)T 1 + (219. - 155. i)T
good3 1+(−0.991−0.991i)T+9iT2 1 + (-0.991 - 0.991i)T + 9iT^{2}
5 1+6.41T+25T2 1 + 6.41T + 25T^{2}
7 1+(6.33−6.33i)T−49iT2 1 + (6.33 - 6.33i)T - 49iT^{2}
11 1−6.36iT−121T2 1 - 6.36iT - 121T^{2}
13 1+22.5iT−169T2 1 + 22.5iT - 169T^{2}
17 1+(1.76+1.76i)T+289iT2 1 + (1.76 + 1.76i)T + 289iT^{2}
19 1+(−21.8+21.8i)T−361iT2 1 + (-21.8 + 21.8i)T - 361iT^{2}
23 1−10.5T+529T2 1 - 10.5T + 529T^{2}
29 1+(15.1−15.1i)T−841iT2 1 + (15.1 - 15.1i)T - 841iT^{2}
31 1+(−1.42+1.42i)T−961iT2 1 + (-1.42 + 1.42i)T - 961iT^{2}
37 1+51.9T+1.36e3T2 1 + 51.9T + 1.36e3T^{2}
41 1+28.6T+1.68e3T2 1 + 28.6T + 1.68e3T^{2}
43 1+49.5iT−1.84e3T2 1 + 49.5iT - 1.84e3T^{2}
47 1+57.7T+2.20e3T2 1 + 57.7T + 2.20e3T^{2}
53 1−20.7T+2.80e3T2 1 - 20.7T + 2.80e3T^{2}
59 1+(38.8−38.8i)T−3.48e3iT2 1 + (38.8 - 38.8i)T - 3.48e3iT^{2}
61 1+110.T+3.72e3T2 1 + 110.T + 3.72e3T^{2}
67 1+80.9T+4.48e3T2 1 + 80.9T + 4.48e3T^{2}
71 1+(−34.1+34.1i)T−5.04e3iT2 1 + (-34.1 + 34.1i)T - 5.04e3iT^{2}
73 1−3.81iT−5.32e3T2 1 - 3.81iT - 5.32e3T^{2}
79 1−62.5iT−6.24e3T2 1 - 62.5iT - 6.24e3T^{2}
83 1+(−55.4+55.4i)T−6.88e3iT2 1 + (-55.4 + 55.4i)T - 6.88e3iT^{2}
89 1+78.4iT−7.92e3T2 1 + 78.4iT - 7.92e3T^{2}
97 1+42.6iT−9.40e3T2 1 + 42.6iT - 9.40e3T^{2}
show more
show less
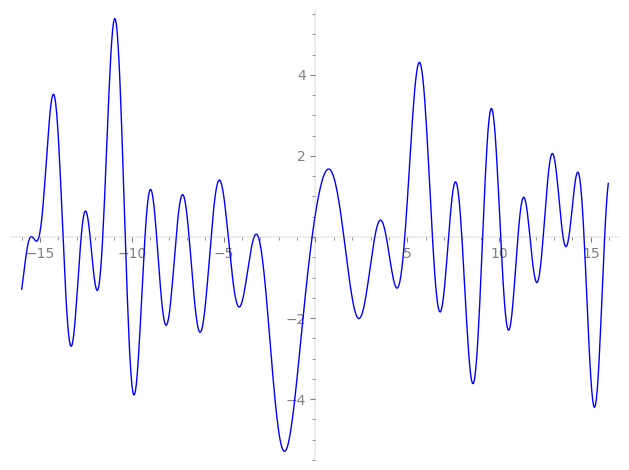
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.36025954836195047674373975914, −9.286411958846838136418105742103, −8.650933762325230164945078133649, −7.58798490695578250026068055013, −6.88337353434862238402948879981, −5.68319146633123051734548587178, −4.74894805227220285245321342598, −3.34228715168736484937896129537, −3.11044066753158905758004133749, −0.18376825165047844610796146593, 1.54852822126656550194672512865, 3.23052924517527015891164063763, 3.85722455824050093415146676074, 4.86541051821778984855117740800, 6.37210674803740797147185008422, 7.25178561628261495919797217884, 7.974513932306546381743877707093, 9.106310004667486199987392043960, 10.09072552100877206815568427143, 11.02949414040131225628762793361

Graph of the ZZ-function along the critical line