↑

Properties

Label 2-630-35.3-c1-0-18
Degree 22
Conductor 630630
Sign 0.616+0.787i0.616 + 0.787i
Analytic cond. 5.030575.03057
Root an. cond. 2.242892.24289
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.965 + 0.258i)2-s + (0.866 + 0.499i)4-s + (−2.20 − 0.378i)5-s + (0.126 − 2.64i)7-s + (0.707 + 0.707i)8-s + (−2.03 − 0.935i)10-s + (2.81 − 4.87i)11-s + (−1.42 + 1.42i)13-s + (0.806 − 2.51i)14-s + (0.500 + 0.866i)16-s + (5.12 − 1.37i)17-s + (−1.94 − 3.37i)19-s + (−1.71 − 1.42i)20-s + (3.97 − 3.97i)22-s + (0.290 − 1.08i)23-s + ⋯
L(s)  = 1  + (0.683 + 0.183i)2-s + (0.433 + 0.249i)4-s + (−0.985 − 0.169i)5-s + (0.0477 − 0.998i)7-s + (0.249 + 0.249i)8-s + (−0.642 − 0.295i)10-s + (0.848 − 1.46i)11-s + (−0.396 + 0.396i)13-s + (0.215 − 0.673i)14-s + (0.125 + 0.216i)16-s + (1.24 − 0.333i)17-s + (−0.446 − 0.773i)19-s + (−0.384 − 0.319i)20-s + (0.848 − 0.848i)22-s + (0.0606 − 0.226i)23-s + ⋯

Functional equation

Λ(s)=(630s/2 ΓC(s) L(s)=((0.616+0.787i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 630 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.616 + 0.787i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(630s/2 ΓC(s+1/2) L(s)=((0.616+0.787i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 630 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.616 + 0.787i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 630630    =    2⋅32⋅5⋅72 \cdot 3^{2} \cdot 5 \cdot 7
Sign: 0.616+0.787i0.616 + 0.787i
Analytic conductor: 5.030575.03057
Root analytic conductor: 2.242892.24289
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ630(73,⋅)\chi_{630} (73, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 630, ( :1/2), 0.616+0.787i)(2,\ 630,\ (\ :1/2),\ 0.616 + 0.787i)

Particular Values

L(1)L(1) ≈\approx 1.67633−0.816427i1.67633 - 0.816427i
L(12)L(\frac12) ≈\approx 1.67633−0.816427i1.67633 - 0.816427i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(−0.965−0.258i)T 1 + (-0.965 - 0.258i)T
3 1 1
5 1+(2.20+0.378i)T 1 + (2.20 + 0.378i)T
7 1+(−0.126+2.64i)T 1 + (-0.126 + 2.64i)T
good11 1+(−2.81+4.87i)T+(−5.5−9.52i)T2 1 + (-2.81 + 4.87i)T + (-5.5 - 9.52i)T^{2}
13 1+(1.42−1.42i)T−13iT2 1 + (1.42 - 1.42i)T - 13iT^{2}
17 1+(−5.12+1.37i)T+(14.7−8.5i)T2 1 + (-5.12 + 1.37i)T + (14.7 - 8.5i)T^{2}
19 1+(1.94+3.37i)T+(−9.5+16.4i)T2 1 + (1.94 + 3.37i)T + (-9.5 + 16.4i)T^{2}
23 1+(−0.290+1.08i)T+(−19.9−11.5i)T2 1 + (-0.290 + 1.08i)T + (-19.9 - 11.5i)T^{2}
29 1+3.15iT−29T2 1 + 3.15iT - 29T^{2}
31 1+(3.33+1.92i)T+(15.5+26.8i)T2 1 + (3.33 + 1.92i)T + (15.5 + 26.8i)T^{2}
37 1+(−4.86−1.30i)T+(32.0+18.5i)T2 1 + (-4.86 - 1.30i)T + (32.0 + 18.5i)T^{2}
41 1−7.21iT−41T2 1 - 7.21iT - 41T^{2}
43 1+(−1.85−1.85i)T+43iT2 1 + (-1.85 - 1.85i)T + 43iT^{2}
47 1+(−1.52+5.69i)T+(−40.7−23.5i)T2 1 + (-1.52 + 5.69i)T + (-40.7 - 23.5i)T^{2}
53 1+(1.33−0.357i)T+(45.8−26.5i)T2 1 + (1.33 - 0.357i)T + (45.8 - 26.5i)T^{2}
59 1+(2.73−4.74i)T+(−29.5−51.0i)T2 1 + (2.73 - 4.74i)T + (-29.5 - 51.0i)T^{2}
61 1+(3.99−2.30i)T+(30.5−52.8i)T2 1 + (3.99 - 2.30i)T + (30.5 - 52.8i)T^{2}
67 1+(−0.218−0.816i)T+(−58.0+33.5i)T2 1 + (-0.218 - 0.816i)T + (-58.0 + 33.5i)T^{2}
71 1+4.77T+71T2 1 + 4.77T + 71T^{2}
73 1+(−1.45−5.42i)T+(−63.2+36.5i)T2 1 + (-1.45 - 5.42i)T + (-63.2 + 36.5i)T^{2}
79 1+(−5.41+3.12i)T+(39.5−68.4i)T2 1 + (-5.41 + 3.12i)T + (39.5 - 68.4i)T^{2}
83 1+(5.67−5.67i)T−83iT2 1 + (5.67 - 5.67i)T - 83iT^{2}
89 1+(−5.96−10.3i)T+(−44.5+77.0i)T2 1 + (-5.96 - 10.3i)T + (-44.5 + 77.0i)T^{2}
97 1+(6.63+6.63i)T+97iT2 1 + (6.63 + 6.63i)T + 97iT^{2}
show more
show less
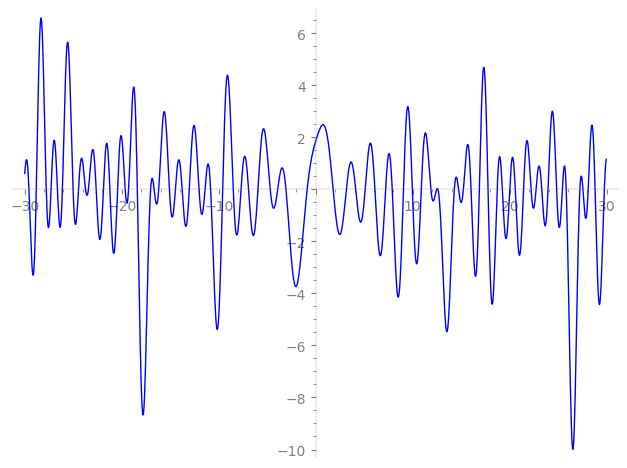
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.83162135268034461660641425103, −9.595114480135332567624275120302, −8.503303115011667397109360701998, −7.69844091800040801968990041004, −6.92239505728064722626002974204, −5.95834567991953290656076991170, −4.68990505693547993220869463860, −3.92100101848708819390041155330, −3.06667558546848547771754561522, −0.882854889155919811856378915011, 1.79629812043631793362247417639, 3.15881057735837057572506694130, 4.12290250454635335395170106837, 5.09620220200329785196342296140, 6.10049592812679091267587042134, 7.20394918562390158014693350190, 7.88624294353729199618812716280, 9.043460504091149440334885187491, 9.958446471718874325351239583660, 10.87953915729989366218249050237

Graph of the ZZ-function along the critical line