↑

Properties

Label 2-735-105.59-c1-0-42
Degree 22
Conductor 735735
Sign 0.982+0.188i0.982 + 0.188i
Analytic cond. 5.869005.86900
Root an. cond. 2.422602.42260
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.701 + 1.21i)2-s + (−1.5 − 0.866i)3-s + (0.0157 − 0.0272i)4-s + (1.93 − 1.11i)5-s − 2.43i·6-s + 2.85·8-s + (1.5 + 2.59i)9-s + (2.71 + 1.56i)10-s + (−0.0472 + 0.0272i)12-s − 3.87·15-s + (1.96 + 3.40i)16-s + (−6.98 − 4.03i)17-s + (−2.10 + 3.64i)18-s + (5.76 − 3.32i)19-s − 0.0704i·20-s + ⋯
L(s)  = 1  + (0.496 + 0.859i)2-s + (−0.866 − 0.499i)3-s + (0.00787 − 0.0136i)4-s + (0.866 − 0.499i)5-s − 0.992i·6-s + 1.00·8-s + (0.5 + 0.866i)9-s + (0.859 + 0.496i)10-s + (−0.0136 + 0.00787i)12-s − 1.00·15-s + (0.491 + 0.852i)16-s + (−1.69 − 0.977i)17-s + (−0.496 + 0.859i)18-s + (1.32 − 0.763i)19-s − 0.0157i·20-s + ⋯

Functional equation

Λ(s)=(735s/2 ΓC(s) L(s)=((0.982+0.188i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 735 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.982 + 0.188i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(735s/2 ΓC(s+1/2) L(s)=((0.982+0.188i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 735 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.982 + 0.188i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 735735    =    3⋅5⋅723 \cdot 5 \cdot 7^{2}
Sign: 0.982+0.188i0.982 + 0.188i
Analytic conductor: 5.869005.86900
Root analytic conductor: 2.422602.42260
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ735(374,⋅)\chi_{735} (374, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 735, ( :1/2), 0.982+0.188i)(2,\ 735,\ (\ :1/2),\ 0.982 + 0.188i)

Particular Values

L(1)L(1) ≈\approx 1.91895−0.182513i1.91895 - 0.182513i
L(12)L(\frac12) ≈\approx 1.91895−0.182513i1.91895 - 0.182513i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad3 1+(1.5+0.866i)T 1 + (1.5 + 0.866i)T
5 1+(−1.93+1.11i)T 1 + (-1.93 + 1.11i)T
7 1 1
good2 1+(−0.701−1.21i)T+(−1+1.73i)T2 1 + (-0.701 - 1.21i)T + (-1 + 1.73i)T^{2}
11 1+(5.5+9.52i)T2 1 + (5.5 + 9.52i)T^{2}
13 1+13T2 1 + 13T^{2}
17 1+(6.98+4.03i)T+(8.5+14.7i)T2 1 + (6.98 + 4.03i)T + (8.5 + 14.7i)T^{2}
19 1+(−5.76+3.32i)T+(9.5−16.4i)T2 1 + (-5.76 + 3.32i)T + (9.5 - 16.4i)T^{2}
23 1+(0.111+0.192i)T+(−11.5+19.9i)T2 1 + (0.111 + 0.192i)T + (-11.5 + 19.9i)T^{2}
29 1−29T2 1 - 29T^{2}
31 1+(−8.84−5.10i)T+(15.5+26.8i)T2 1 + (-8.84 - 5.10i)T + (15.5 + 26.8i)T^{2}
37 1+(18.5−32.0i)T2 1 + (18.5 - 32.0i)T^{2}
41 1+41T2 1 + 41T^{2}
43 1−43T2 1 - 43T^{2}
47 1+(0.886−0.511i)T+(23.5−40.7i)T2 1 + (0.886 - 0.511i)T + (23.5 - 40.7i)T^{2}
53 1+(−5.54+9.60i)T+(−26.5−45.8i)T2 1 + (-5.54 + 9.60i)T + (-26.5 - 45.8i)T^{2}
59 1+(−29.5−51.0i)T2 1 + (-29.5 - 51.0i)T^{2}
61 1+(13.0−7.53i)T+(30.5−52.8i)T2 1 + (13.0 - 7.53i)T + (30.5 - 52.8i)T^{2}
67 1+(33.5+58.0i)T2 1 + (33.5 + 58.0i)T^{2}
71 1−71T2 1 - 71T^{2}
73 1+(−36.5−63.2i)T2 1 + (-36.5 - 63.2i)T^{2}
79 1+(2.91+5.05i)T+(−39.5+68.4i)T2 1 + (2.91 + 5.05i)T + (-39.5 + 68.4i)T^{2}
83 1−15.0iT−83T2 1 - 15.0iT - 83T^{2}
89 1+(−44.5+77.0i)T2 1 + (-44.5 + 77.0i)T^{2}
97 1+97T2 1 + 97T^{2}
show more
show less
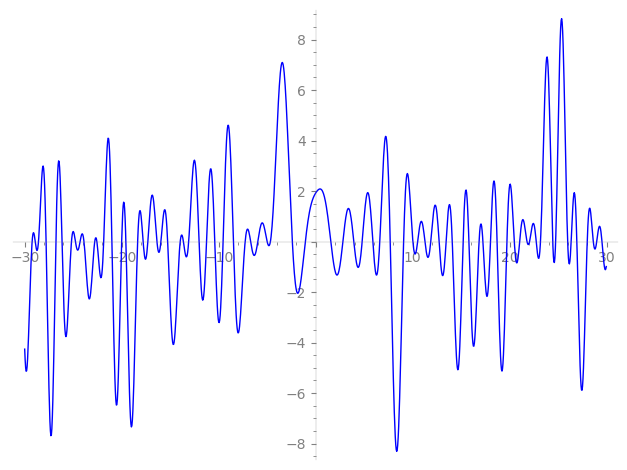
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.40619543048951888408385927793, −9.550011786532002029413263756167, −8.487402118520978122412752119478, −7.27424949617216490460142953521, −6.70864321116137886435947618551, −5.97024156465507578616722291308, −5.00707427160934197894986710117, −4.67238919055432237512579345245, −2.41012262124259710933505301600, −1.06944182156322602394991522636, 1.55599893875830309781945744555, 2.80088856083354210935939408992, 3.92599101477187146245069125615, 4.78602030502439427327725364607, 5.88789743199492640759808375927, 6.60183819434215832765471560444, 7.68037992021194934683674501212, 9.059555977474144378979279061003, 10.01715317723032320004227329080, 10.50703337102210298161302633942

Graph of the ZZ-function along the critical line