↑

Properties

Label 2-735-105.59-c1-0-6
Degree 22
Conductor 735735
Sign 0.797+0.603i0.797 + 0.603i
Analytic cond. 5.869005.86900
Root an. cond. 2.422602.42260
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−1.10 − 1.91i)2-s + (−1.38 + 1.04i)3-s + (−1.43 + 2.49i)4-s + (−2.22 − 0.255i)5-s + (3.52 + 1.48i)6-s + 1.94·8-s + (0.810 − 2.88i)9-s + (1.96 + 4.53i)10-s + (−3.30 − 1.90i)11-s + (−0.622 − 4.94i)12-s − 6.50·13-s + (3.33 − 1.97i)15-s + (0.732 + 1.26i)16-s + (2.54 + 1.47i)17-s + (−6.42 + 1.64i)18-s + (−1.76 + 1.01i)19-s + ⋯
L(s)  = 1  + (−0.781 − 1.35i)2-s + (−0.796 + 0.604i)3-s + (−0.719 + 1.24i)4-s + (−0.993 − 0.114i)5-s + (1.43 + 0.606i)6-s + 0.687·8-s + (0.270 − 0.962i)9-s + (0.621 + 1.43i)10-s + (−0.996 − 0.575i)11-s + (−0.179 − 1.42i)12-s − 1.80·13-s + (0.860 − 0.509i)15-s + (0.183 + 0.317i)16-s + (0.617 + 0.356i)17-s + (−1.51 + 0.386i)18-s + (−0.404 + 0.233i)19-s + ⋯

Functional equation

Λ(s)=(735s/2 ΓC(s) L(s)=((0.797+0.603i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 735 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.797 + 0.603i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(735s/2 ΓC(s+1/2) L(s)=((0.797+0.603i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 735 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (0.797 + 0.603i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 735735    =    3⋅5⋅723 \cdot 5 \cdot 7^{2}
Sign: 0.797+0.603i0.797 + 0.603i
Analytic conductor: 5.869005.86900
Root analytic conductor: 2.422602.42260
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ735(374,⋅)\chi_{735} (374, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 735, ( :1/2), 0.797+0.603i)(2,\ 735,\ (\ :1/2),\ 0.797 + 0.603i)

Particular Values

L(1)L(1) ≈\approx 0.289189−0.0970738i0.289189 - 0.0970738i
L(12)L(\frac12) ≈\approx 0.289189−0.0970738i0.289189 - 0.0970738i
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad3 1+(1.38−1.04i)T 1 + (1.38 - 1.04i)T
5 1+(2.22+0.255i)T 1 + (2.22 + 0.255i)T
7 1 1
good2 1+(1.10+1.91i)T+(−1+1.73i)T2 1 + (1.10 + 1.91i)T + (-1 + 1.73i)T^{2}
11 1+(3.30+1.90i)T+(5.5+9.52i)T2 1 + (3.30 + 1.90i)T + (5.5 + 9.52i)T^{2}
13 1+6.50T+13T2 1 + 6.50T + 13T^{2}
17 1+(−2.54−1.47i)T+(8.5+14.7i)T2 1 + (-2.54 - 1.47i)T + (8.5 + 14.7i)T^{2}
19 1+(1.76−1.01i)T+(9.5−16.4i)T2 1 + (1.76 - 1.01i)T + (9.5 - 16.4i)T^{2}
23 1+(1.50+2.59i)T+(−11.5+19.9i)T2 1 + (1.50 + 2.59i)T + (-11.5 + 19.9i)T^{2}
29 1−2.25iT−29T2 1 - 2.25iT - 29T^{2}
31 1+(−5.77−3.33i)T+(15.5+26.8i)T2 1 + (-5.77 - 3.33i)T + (15.5 + 26.8i)T^{2}
37 1+(−2.91+1.68i)T+(18.5−32.0i)T2 1 + (-2.91 + 1.68i)T + (18.5 - 32.0i)T^{2}
41 1+3.51T+41T2 1 + 3.51T + 41T^{2}
43 1+7.03iT−43T2 1 + 7.03iT - 43T^{2}
47 1+(−4.34+2.50i)T+(23.5−40.7i)T2 1 + (-4.34 + 2.50i)T + (23.5 - 40.7i)T^{2}
53 1+(0.967−1.67i)T+(−26.5−45.8i)T2 1 + (0.967 - 1.67i)T + (-26.5 - 45.8i)T^{2}
59 1+(3.96−6.86i)T+(−29.5−51.0i)T2 1 + (3.96 - 6.86i)T + (-29.5 - 51.0i)T^{2}
61 1+(−11.8+6.83i)T+(30.5−52.8i)T2 1 + (-11.8 + 6.83i)T + (30.5 - 52.8i)T^{2}
67 1+(−9.34−5.39i)T+(33.5+58.0i)T2 1 + (-9.34 - 5.39i)T + (33.5 + 58.0i)T^{2}
71 1−10.9iT−71T2 1 - 10.9iT - 71T^{2}
73 1+(−1.65+2.86i)T+(−36.5−63.2i)T2 1 + (-1.65 + 2.86i)T + (-36.5 - 63.2i)T^{2}
79 1+(−2.92−5.06i)T+(−39.5+68.4i)T2 1 + (-2.92 - 5.06i)T + (-39.5 + 68.4i)T^{2}
83 1−2.66iT−83T2 1 - 2.66iT - 83T^{2}
89 1+(6.75+11.7i)T+(−44.5+77.0i)T2 1 + (6.75 + 11.7i)T + (-44.5 + 77.0i)T^{2}
97 1+4.46T+97T2 1 + 4.46T + 97T^{2}
show more
show less
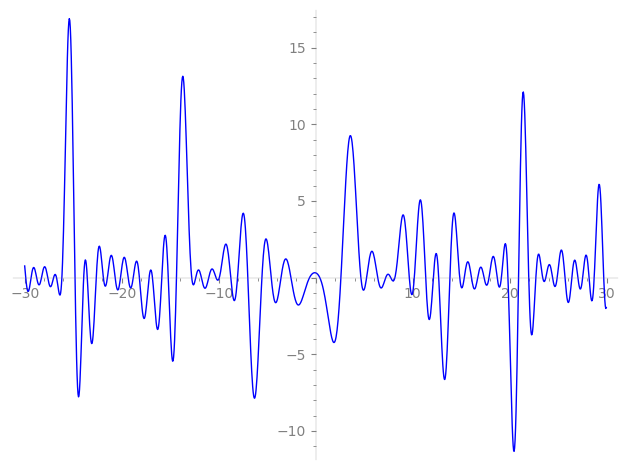
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.28129618448427905566558015969, −9.936138758011543092565284732338, −8.760480673245069120803008108525, −8.060933354473876652696718778631, −6.99901858464522817885006214235, −5.54596487864892249880547160198, −4.58802730482168263628121281497, −3.57858517111664520712730483978, −2.55485200474944397392278528292, −0.63280970994829087904061401168, 0.41496849333041086863742347426, 2.59645819265375800404136052744, 4.65468304904873522189462576243, 5.24407327820315262362544839306, 6.38657122904140315148745566075, 7.21618181675760672024633387040, 7.72604643612377042900674756014, 8.163013074471608194934146616267, 9.645000788184025297967991238134, 10.16212838743685963097852901226

Graph of the ZZ-function along the critical line