↑

Properties

Label 2-800-5.3-c2-0-31
Degree 22
Conductor 800800
Sign 0.130+0.991i0.130 + 0.991i
Analytic cond. 21.798421.7984
Root an. cond. 4.668874.66887
Motivic weight 22
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (1.54 + 1.54i)3-s + (2 − 2i)7-s − 4.19i·9-s − 1.10·11-s + (−10.0 − 10.0i)13-s + (−3.91 + 3.91i)17-s − 23.3i·19-s + 6.19·21-s + (−5.29 − 5.29i)23-s + (20.4 − 20.4i)27-s − 32.5i·29-s − 42.3·31-s + (−1.70 − 1.70i)33-s + (−22.2 + 22.2i)37-s − 31.1i·39-s + ⋯
L(s)  = 1  + (0.516 + 0.516i)3-s + (0.285 − 0.285i)7-s − 0.466i·9-s − 0.100·11-s + (−0.772 − 0.772i)13-s + (−0.230 + 0.230i)17-s − 1.23i·19-s + 0.295·21-s + (−0.230 − 0.230i)23-s + (0.757 − 0.757i)27-s − 1.12i·29-s − 1.36·31-s + (−0.0518 − 0.0518i)33-s + (−0.602 + 0.602i)37-s − 0.797i·39-s + ⋯

Functional equation

Λ(s)=(800s/2 ΓC(s) L(s)=((0.130+0.991i) Λ‾(3−s)\begin{aligned}\Lambda(s)=\mathstrut & 800 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.130 + 0.991i)\, \overline{\Lambda}(3-s) \end{aligned}
Λ(s)=(800s/2 ΓC(s+1) L(s)=((0.130+0.991i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 800 ^{s/2} \, \Gamma_{\C}(s+1) \, L(s)\cr =\mathstrut & (0.130 + 0.991i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 800800    =    25⋅522^{5} \cdot 5^{2}
Sign: 0.130+0.991i0.130 + 0.991i
Analytic conductor: 21.798421.7984
Root analytic conductor: 4.668874.66887
Motivic weight: 22
Rational: no
Arithmetic: yes
Character: χ800(193,⋅)\chi_{800} (193, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 800, ( :1), 0.130+0.991i)(2,\ 800,\ (\ :1),\ 0.130 + 0.991i)

Particular Values

L(32)L(\frac{3}{2}) ≈\approx 1.6052286581.605228658
L(12)L(\frac12) ≈\approx 1.6052286581.605228658
L(2)L(2) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
5 1 1
good3 1+(−1.54−1.54i)T+9iT2 1 + (-1.54 - 1.54i)T + 9iT^{2}
7 1+(−2+2i)T−49iT2 1 + (-2 + 2i)T - 49iT^{2}
11 1+1.10T+121T2 1 + 1.10T + 121T^{2}
13 1+(10.0+10.0i)T+169iT2 1 + (10.0 + 10.0i)T + 169iT^{2}
17 1+(3.91−3.91i)T−289iT2 1 + (3.91 - 3.91i)T - 289iT^{2}
19 1+23.3iT−361T2 1 + 23.3iT - 361T^{2}
23 1+(5.29+5.29i)T+529iT2 1 + (5.29 + 5.29i)T + 529iT^{2}
29 1+32.5iT−841T2 1 + 32.5iT - 841T^{2}
31 1+42.3T+961T2 1 + 42.3T + 961T^{2}
37 1+(22.2−22.2i)T−1.36e3iT2 1 + (22.2 - 22.2i)T - 1.36e3iT^{2}
41 1+15T+1.68e3T2 1 + 15T + 1.68e3T^{2}
43 1+(−32.5−32.5i)T+1.84e3iT2 1 + (-32.5 - 32.5i)T + 1.84e3iT^{2}
47 1+(−55.2+55.2i)T−2.20e3iT2 1 + (-55.2 + 55.2i)T - 2.20e3iT^{2}
53 1+(16.6+16.6i)T+2.80e3iT2 1 + (16.6 + 16.6i)T + 2.80e3iT^{2}
59 1+111.iT−3.48e3T2 1 + 111. iT - 3.48e3T^{2}
61 1−5.40T+3.72e3T2 1 - 5.40T + 3.72e3T^{2}
67 1+(−36.0+36.0i)T−4.48e3iT2 1 + (-36.0 + 36.0i)T - 4.48e3iT^{2}
71 1+71.2T+5.04e3T2 1 + 71.2T + 5.04e3T^{2}
73 1+(−93.0−93.0i)T+5.32e3iT2 1 + (-93.0 - 93.0i)T + 5.32e3iT^{2}
79 1+118.iT−6.24e3T2 1 + 118. iT - 6.24e3T^{2}
83 1+(−6.64−6.64i)T+6.88e3iT2 1 + (-6.64 - 6.64i)T + 6.88e3iT^{2}
89 1−126.iT−7.92e3T2 1 - 126. iT - 7.92e3T^{2}
97 1+(−73.4+73.4i)T−9.40e3iT2 1 + (-73.4 + 73.4i)T - 9.40e3iT^{2}
show more
show less
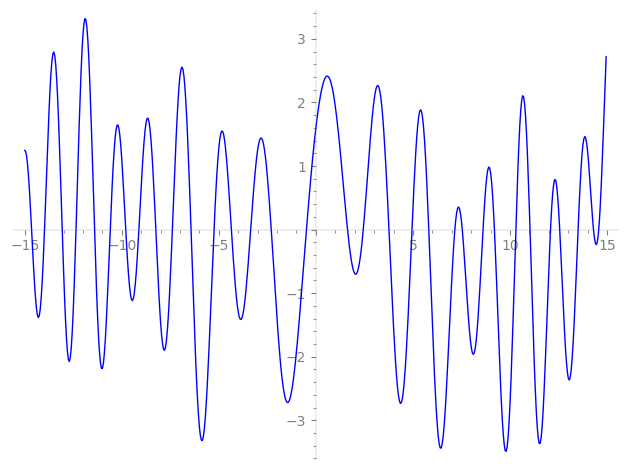
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−9.795335211540416197006605538472, −9.117760665930688620730738444755, −8.245381059390656935350543941761, −7.39362459079578174260720989083, −6.43231129009266935587379104870, −5.24722602517486059033427119099, −4.35305363253888585211965728376, −3.35940517983085051601561789155, −2.30012610319989244549339433936, −0.48725259127449459632563834249, 1.62921792043336268037728475492, 2.43980582855695764931656499607, 3.76311808565655129789417224798, 4.94798096790796964658716784308, 5.81372743008433542495962213225, 7.15662018143369750157651818137, 7.53880371349941586259405808014, 8.608435260180344411460731328575, 9.195476095605219739560669922870, 10.29909243237799362146040351957

Graph of the ZZ-function along the critical line