↑

Properties

Label 4-800e2-1.1-c3e2-0-2
Degree 44
Conductor 640000640000
Sign 11
Analytic cond. 2227.982227.98
Root an. cond. 6.870336.87033
Motivic weight 33
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

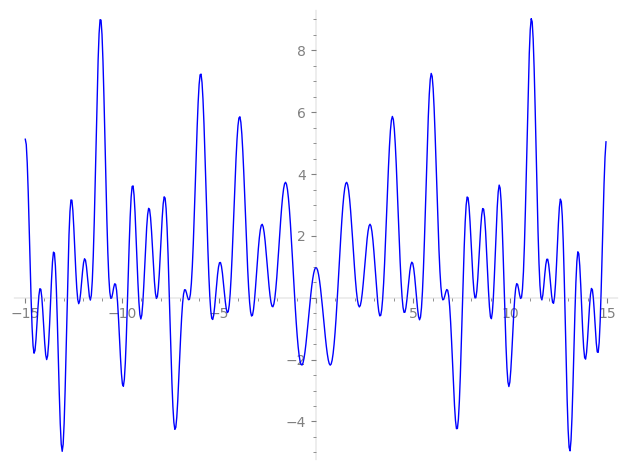
L(s)  = 1  − 14·9-s − 76·13-s − 68·17-s + 540·29-s − 412·37-s − 540·41-s − 326·49-s + 516·53-s − 500·61-s + 2.15e3·73-s − 533·81-s + 1.78e3·89-s + 508·97-s + 1.19e3·101-s + 1.70e3·109-s − 3.39e3·113-s + 1.06e3·117-s − 2.50e3·121-s + 127-s + 131-s + 137-s + 139-s + 149-s + 151-s + 952·153-s + 157-s + 163-s + ⋯
L(s)  = 1  − 0.518·9-s − 1.62·13-s − 0.970·17-s + 3.45·29-s − 1.83·37-s − 2.05·41-s − 0.950·49-s + 1.33·53-s − 1.04·61-s + 3.45·73-s − 0.731·81-s + 2.11·89-s + 0.531·97-s + 1.17·101-s + 1.50·109-s − 2.82·113-s + 0.840·117-s − 1.87·121-s + 0.000698·127-s + 0.000666·131-s + 0.000623·137-s + 0.000610·139-s + 0.000549·149-s + 0.000538·151-s + 0.503·153-s + 0.000508·157-s + 0.000480·163-s + ⋯

Functional equation

Λ(s)=(640000s/2 ΓC(s)2 L(s)=( Λ(4−s)\begin{aligned}\Lambda(s)=\mathstrut & 640000 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(4-s) \end{aligned}
Λ(s)=(640000s/2 ΓC(s+3/2)2 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 640000 ^{s/2} \, \Gamma_{\C}(s+3/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 44
Conductor: 640000640000    =    210⋅542^{10} \cdot 5^{4}
Sign: 11
Analytic conductor: 2227.982227.98
Root analytic conductor: 6.870336.87033
Motivic weight: 33
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (4, 640000, ( :3/2,3/2), 1)(4,\ 640000,\ (\ :3/2, 3/2),\ 1)

Particular Values

L(2)L(2) ≈\approx 0.98013631520.9801363152
L(12)L(\frac12) ≈\approx 0.98013631520.9801363152
L(52)L(\frac{5}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2 1 1
5 1 1
good3C22C_2^2 1+14T2+p6T4 1 + 14 T^{2} + p^{6} T^{4}
7C22C_2^2 1+326T2+p6T4 1 + 326 T^{2} + p^{6} T^{4}
11C22C_2^2 1+2502T2+p6T4 1 + 2502 T^{2} + p^{6} T^{4}
13C2C_2 (1+38T+p3T2)2 ( 1 + 38 T + p^{3} T^{2} )^{2}
17C2C_2 (1+2pT+p3T2)2 ( 1 + 2 p T + p^{3} T^{2} )^{2}
19C22C_2^2 1+3478T2+p6T4 1 + 3478 T^{2} + p^{6} T^{4}
23C22C_2^2 1+17574T2+p6T4 1 + 17574 T^{2} + p^{6} T^{4}
29C2C_2 (1−270T+p3T2)2 ( 1 - 270 T + p^{3} T^{2} )^{2}
31C22C_2^2 1−57058T2+p6T4 1 - 57058 T^{2} + p^{6} T^{4}
37C2C_2 (1+206T+p3T2)2 ( 1 + 206 T + p^{3} T^{2} )^{2}
41C2C_2 (1+270T+p3T2)2 ( 1 + 270 T + p^{3} T^{2} )^{2}
43C22C_2^2 1−129986T2+p6T4 1 - 129986 T^{2} + p^{6} T^{4}
47C22C_2^2 1+190006T2+p6T4 1 + 190006 T^{2} + p^{6} T^{4}
53C2C_2 (1−258T+p3T2)2 ( 1 - 258 T + p^{3} T^{2} )^{2}
59C22C_2^2 1+404998T2+p6T4 1 + 404998 T^{2} + p^{6} T^{4}
61C2C_2 (1+250T+p3T2)2 ( 1 + 250 T + p^{3} T^{2} )^{2}
67C22C_2^2 1−64114T2+p6T4 1 - 64114 T^{2} + p^{6} T^{4}
71C22C_2^2 1+299662T2+p6T4 1 + 299662 T^{2} + p^{6} T^{4}
73C2C_2 (1−1078T+p3T2)2 ( 1 - 1078 T + p^{3} T^{2} )^{2}
79C22C_2^2 1+908638T2+p6T4 1 + 908638 T^{2} + p^{6} T^{4}
83C22C_2^2 1−81426T2+p6T4 1 - 81426 T^{2} + p^{6} T^{4}
89C2C_2 (1−10pT+p3T2)2 ( 1 - 10 p T + p^{3} T^{2} )^{2}
97C2C_2 (1−254T+p3T2)2 ( 1 - 254 T + p^{3} T^{2} )^{2}
show more
show less
   L(s)=∏p ∏j=14(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−10.23451933887939789669805235536, −9.701997660618840758960782394623, −9.131569080247708413189564627381, −8.900962433995662839984440889367, −8.231376333426647150968870971040, −8.179912953935986957600017457681, −7.55056901872421358901105903769, −6.84315727494272367078024195662, −6.60619216345694006662681261185, −6.49552164182341887712946692670, −5.46446838164856402271630170695, −5.17645615559185625847641613917, −4.69133480429537558933889286481, −4.43395999108753006251037357154, −3.43643670057893878187351628298, −3.15688626071505511407028331992, −2.35348824279759641073464597163, −2.11820551253215544693149834386, −1.09796248706382642042406981247, −0.28523851105051543404136060878, 0.28523851105051543404136060878, 1.09796248706382642042406981247, 2.11820551253215544693149834386, 2.35348824279759641073464597163, 3.15688626071505511407028331992, 3.43643670057893878187351628298, 4.43395999108753006251037357154, 4.69133480429537558933889286481, 5.17645615559185625847641613917, 5.46446838164856402271630170695, 6.49552164182341887712946692670, 6.60619216345694006662681261185, 6.84315727494272367078024195662, 7.55056901872421358901105903769, 8.179912953935986957600017457681, 8.231376333426647150968870971040, 8.900962433995662839984440889367, 9.131569080247708413189564627381, 9.701997660618840758960782394623, 10.23451933887939789669805235536

Graph of the ZZ-function along the critical line