↑

Properties

Label 4-816e2-1.1-c3e2-0-1
Degree 44
Conductor 665856665856
Sign 11
Analytic cond. 2317.992317.99
Root an. cond. 6.938706.93870
Motivic weight 33
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

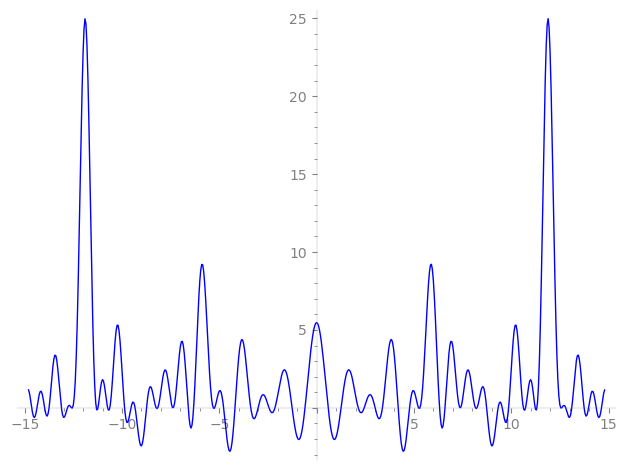
L(s)  = 1  + 6·3-s + 6·5-s + 8·7-s + 27·9-s − 66·11-s − 2·13-s + 36·15-s − 34·17-s + 26·19-s + 48·21-s + 198·23-s + 65·25-s + 108·27-s + 444·29-s − 532·31-s − 396·33-s + 48·35-s + 88·37-s − 12·39-s + 570·41-s + 182·43-s + 162·45-s − 420·47-s − 350·49-s − 204·51-s − 300·53-s − 396·55-s + ⋯
L(s)  = 1  + 1.15·3-s + 0.536·5-s + 0.431·7-s + 9-s − 1.80·11-s − 0.0426·13-s + 0.619·15-s − 0.485·17-s + 0.313·19-s + 0.498·21-s + 1.79·23-s + 0.519·25-s + 0.769·27-s + 2.84·29-s − 3.08·31-s − 2.08·33-s + 0.231·35-s + 0.391·37-s − 0.0492·39-s + 2.17·41-s + 0.645·43-s + 0.536·45-s − 1.30·47-s − 1.02·49-s − 0.560·51-s − 0.777·53-s − 0.970·55-s + ⋯

Functional equation

Λ(s)=(665856s/2 ΓC(s)2 L(s)=( Λ(4−s)\begin{aligned}\Lambda(s)=\mathstrut & 665856 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(4-s) \end{aligned}
Λ(s)=(665856s/2 ΓC(s+3/2)2 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 665856 ^{s/2} \, \Gamma_{\C}(s+3/2)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 44
Conductor: 665856665856    =    28⋅32⋅1722^{8} \cdot 3^{2} \cdot 17^{2}
Sign: 11
Analytic conductor: 2317.992317.99
Root analytic conductor: 6.938706.93870
Motivic weight: 33
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (4, 665856, ( :3/2,3/2), 1)(4,\ 665856,\ (\ :3/2, 3/2),\ 1)

Particular Values

L(2)L(2) ≈\approx 5.4759231305.475923130
L(12)L(\frac12) ≈\approx 5.4759231305.475923130
L(52)L(\frac{5}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2 1 1
3C1C_1 (1−pT)2 ( 1 - p T )^{2}
17C1C_1 (1+pT)2 ( 1 + p T )^{2}
good5D4D_{4} 1−6T−29T2−6p3T3+p6T4 1 - 6 T - 29 T^{2} - 6 p^{3} T^{3} + p^{6} T^{4}
7D4D_{4} 1−8T+414T2−8p3T3+p6T4 1 - 8 T + 414 T^{2} - 8 p^{3} T^{3} + p^{6} T^{4}
11D4D_{4} 1+6pT+3463T2+6p4T3+p6T4 1 + 6 p T + 3463 T^{2} + 6 p^{4} T^{3} + p^{6} T^{4}
13D4D_{4} 1+2T+3243T2+2p3T3+p6T4 1 + 2 T + 3243 T^{2} + 2 p^{3} T^{3} + p^{6} T^{4}
19D4D_{4} 1−26T+9279T2−26p3T3+p6T4 1 - 26 T + 9279 T^{2} - 26 p^{3} T^{3} + p^{6} T^{4}
23D4D_{4} 1−198T+33847T2−198p3T3+p6T4 1 - 198 T + 33847 T^{2} - 198 p^{3} T^{3} + p^{6} T^{4}
29D4D_{4} 1−444T+93454T2−444p3T3+p6T4 1 - 444 T + 93454 T^{2} - 444 p^{3} T^{3} + p^{6} T^{4}
31D4D_{4} 1+532T+129186T2+532p3T3+p6T4 1 + 532 T + 129186 T^{2} + 532 p^{3} T^{3} + p^{6} T^{4}
37D4D_{4} 1−88T+29514T2−88p3T3+p6T4 1 - 88 T + 29514 T^{2} - 88 p^{3} T^{3} + p^{6} T^{4}
41D4D_{4} 1−570T+195739T2−570p3T3+p6T4 1 - 570 T + 195739 T^{2} - 570 p^{3} T^{3} + p^{6} T^{4}
43D4D_{4} 1−182T+162687T2−182p3T3+p6T4 1 - 182 T + 162687 T^{2} - 182 p^{3} T^{3} + p^{6} T^{4}
47D4D_{4} 1+420T+249154T2+420p3T3+p6T4 1 + 420 T + 249154 T^{2} + 420 p^{3} T^{3} + p^{6} T^{4}
53D4D_{4} 1+300T+43486T2+300p3T3+p6T4 1 + 300 T + 43486 T^{2} + 300 p^{3} T^{3} + p^{6} T^{4}
59D4D_{4} 1+444T+294154T2+444p3T3+p6T4 1 + 444 T + 294154 T^{2} + 444 p^{3} T^{3} + p^{6} T^{4}
61D4D_{4} 1−400T+55914T2−400p3T3+p6T4 1 - 400 T + 55914 T^{2} - 400 p^{3} T^{3} + p^{6} T^{4}
67D4D_{4} 1−968T+742470T2−968p3T3+p6T4 1 - 968 T + 742470 T^{2} - 968 p^{3} T^{3} + p^{6} T^{4}
71D4D_{4} 1−1848T+1513150T2−1848p3T3+p6T4 1 - 1848 T + 1513150 T^{2} - 1848 p^{3} T^{3} + p^{6} T^{4}
73D4D_{4} 1−868T+963798T2−868p3T3+p6T4 1 - 868 T + 963798 T^{2} - 868 p^{3} T^{3} + p^{6} T^{4}
79C2C_2 (1+254T+p3T2)2 ( 1 + 254 T + p^{3} T^{2} )^{2}
83D4D_{4} 1+12pT+1388986T2+12p4T3+p6T4 1 + 12 p T + 1388986 T^{2} + 12 p^{4} T^{3} + p^{6} T^{4}
89D4D_{4} 1+288T+287602T2+288p3T3+p6T4 1 + 288 T + 287602 T^{2} + 288 p^{3} T^{3} + p^{6} T^{4}
97D4D_{4} 1−1024T+2038818T2−1024p3T3+p6T4 1 - 1024 T + 2038818 T^{2} - 1024 p^{3} T^{3} + p^{6} T^{4}
show more
show less
   L(s)=∏p ∏j=14(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−9.867524621875145021490405161122, −9.539530189297787365130959988724, −9.326575235248236713787547450084, −8.739430480933774683682437742660, −8.241935812489843689771078972203, −8.164718355711679463740583704887, −7.38884366348938379196404866598, −7.37288929107470924224065553371, −6.59691323272191981227127743911, −6.32012573332259333555707296740, −5.30913339743556374694414010919, −5.24024795078398242309622300718, −4.77636126636573459393378003116, −4.19365471440703557549245284298, −3.38273514131425903126774830768, −3.00730320549634443764432716870, −2.44495371971793750953314431637, −2.14136375086305265634130521952, −1.25786358721961424135900693925, −0.59541988677432637702061280445, 0.59541988677432637702061280445, 1.25786358721961424135900693925, 2.14136375086305265634130521952, 2.44495371971793750953314431637, 3.00730320549634443764432716870, 3.38273514131425903126774830768, 4.19365471440703557549245284298, 4.77636126636573459393378003116, 5.24024795078398242309622300718, 5.30913339743556374694414010919, 6.32012573332259333555707296740, 6.59691323272191981227127743911, 7.37288929107470924224065553371, 7.38884366348938379196404866598, 8.164718355711679463740583704887, 8.241935812489843689771078972203, 8.739430480933774683682437742660, 9.326575235248236713787547450084, 9.539530189297787365130959988724, 9.867524621875145021490405161122

Graph of the ZZ-function along the critical line