↑

Properties

Label 2-820-820.423-c0-0-0
Degree $2$
Conductor $820$
Sign $0.656 + 0.754i$
Analytic cond. $0.409233$
Root an. cond. $0.639713$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−0.951 + 0.309i)2-s + (0.809 − 0.587i)4-s + (0.453 − 0.891i)5-s + (−0.587 + 0.809i)8-s + (0.707 − 0.707i)9-s + (−0.156 + 0.987i)10-s + (−1.26 − 1.47i)13-s + (0.309 − 0.951i)16-s + (0.678 + 1.10i)17-s + (−0.453 + 0.891i)18-s + (−0.156 − 0.987i)20-s + (−0.587 − 0.809i)25-s + (1.65 + 1.01i)26-s + (−1.79 + 0.431i)29-s + i·32-s + ⋯
L(s)  = 1  + (−0.951 + 0.309i)2-s + (0.809 − 0.587i)4-s + (0.453 − 0.891i)5-s + (−0.587 + 0.809i)8-s + (0.707 − 0.707i)9-s + (−0.156 + 0.987i)10-s + (−1.26 − 1.47i)13-s + (0.309 − 0.951i)16-s + (0.678 + 1.10i)17-s + (−0.453 + 0.891i)18-s + (−0.156 − 0.987i)20-s + (−0.587 − 0.809i)25-s + (1.65 + 1.01i)26-s + (−1.79 + 0.431i)29-s + i·32-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 820 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.656 + 0.754i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 820 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.656 + 0.754i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(820\)    =    \(2^{2} \cdot 5 \cdot 41\)
Sign: $0.656 + 0.754i$
Analytic conductor: \(0.409233\)
Root analytic conductor: \(0.639713\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{820} (423, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 820,\ (\ :0),\ 0.656 + 0.754i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.6881232869\)
\(L(\frac12)\) \(\approx\) \(0.6881232869\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (0.951 - 0.309i)T \)
5 \( 1 + (-0.453 + 0.891i)T \)
41 \( 1 + (-0.951 + 0.309i)T \)
good3 \( 1 + (-0.707 + 0.707i)T^{2} \)
7 \( 1 + (-0.987 + 0.156i)T^{2} \)
11 \( 1 + (0.453 - 0.891i)T^{2} \)
13 \( 1 + (1.26 + 1.47i)T + (-0.156 + 0.987i)T^{2} \)
17 \( 1 + (-0.678 - 1.10i)T + (-0.453 + 0.891i)T^{2} \)
19 \( 1 + (0.987 - 0.156i)T^{2} \)
23 \( 1 + (-0.587 - 0.809i)T^{2} \)
29 \( 1 + (1.79 - 0.431i)T + (0.891 - 0.453i)T^{2} \)
31 \( 1 + (0.309 + 0.951i)T^{2} \)
37 \( 1 + (-0.183 + 1.16i)T + (-0.951 - 0.309i)T^{2} \)
43 \( 1 + (0.809 - 0.587i)T^{2} \)
47 \( 1 + (0.987 + 0.156i)T^{2} \)
53 \( 1 + (-1.70 - 1.04i)T + (0.453 + 0.891i)T^{2} \)
59 \( 1 + (-0.809 + 0.587i)T^{2} \)
61 \( 1 + (-0.896 - 1.76i)T + (-0.587 + 0.809i)T^{2} \)
67 \( 1 + (-0.891 + 0.453i)T^{2} \)
71 \( 1 + (-0.453 + 0.891i)T^{2} \)
73 \( 1 - 0.312T + T^{2} \)
79 \( 1 + (0.707 + 0.707i)T^{2} \)
83 \( 1 - iT^{2} \)
89 \( 1 + (0.497 - 0.581i)T + (-0.156 - 0.987i)T^{2} \)
97 \( 1 + (-0.243 - 1.01i)T + (-0.891 + 0.453i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

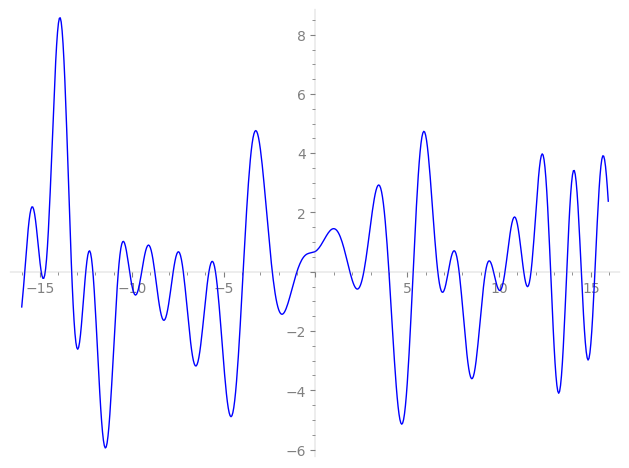
Imaginary part of the first few zeros on the critical line

−10.12298131762112309605626592796, −9.464537311467726271453096533869, −8.752172708876996250341137054578, −7.74854822364332257036662299603, −7.19962477926097944745602597369, −5.80241024018568866816505008234, −5.44639143479321480822509161035, −3.93856776655871429629794651315, −2.35211641019870796640135412539, −1.00929201697721347311449467585, 1.87359634500319362106795455995, 2.63438486039748067285325631525, 4.00207716841804440636961539106, 5.32198172807158643050512940730, 6.66438809018034084003023796861, 7.23521624406168455709189176994, 7.82463370168145983569588110117, 9.263280268752989656464578734842, 9.700069663212240697619981452404, 10.32517196871777397097905464674

Graph of the $Z$-function along the critical line