↑

Properties

Label 2-30e2-20.3-c1-0-37
Degree 22
Conductor 900900
Sign −0.525−0.850i-0.525 - 0.850i
Analytic cond. 7.186537.18653
Root an. cond. 2.680772.68077
Motivic weight 11
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 11

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (−1 − i)2-s + 2i·4-s + (−3 − 3i)7-s + (2 − 2i)8-s + 6i·14-s − 4·16-s + (−1 + i)23-s + (6 − 6i)28-s + 6i·29-s + (4 + 4i)32-s − 12·41-s + (−9 + 9i)43-s + 2·46-s + (−7 − 7i)47-s + 11i·49-s + ⋯
L(s)  = 1  + (−0.707 − 0.707i)2-s + i·4-s + (−1.13 − 1.13i)7-s + (0.707 − 0.707i)8-s + 1.60i·14-s − 16-s + (−0.208 + 0.208i)23-s + (1.13 − 1.13i)28-s + 1.11i·29-s + (0.707 + 0.707i)32-s − 1.87·41-s + (−1.37 + 1.37i)43-s + 0.294·46-s + (−1.02 − 1.02i)47-s + 1.57i·49-s + ⋯

Functional equation

Λ(s)=(900s/2 ΓC(s) L(s)=((−0.525−0.850i) Λ‾(2−s)\begin{aligned}\Lambda(s)=\mathstrut & 900 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.525 - 0.850i)\, \overline{\Lambda}(2-s) \end{aligned}
Λ(s)=(900s/2 ΓC(s+1/2) L(s)=((−0.525−0.850i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 900 ^{s/2} \, \Gamma_{\C}(s+1/2) \, L(s)\cr =\mathstrut & (-0.525 - 0.850i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 900900    =    22⋅32⋅522^{2} \cdot 3^{2} \cdot 5^{2}
Sign: −0.525−0.850i-0.525 - 0.850i
Analytic conductor: 7.186537.18653
Root analytic conductor: 2.680772.68077
Motivic weight: 11
Rational: no
Arithmetic: yes
Character: χ900(343,⋅)\chi_{900} (343, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 11
Selberg data: (2, 900, ( :1/2), −0.525−0.850i)(2,\ 900,\ (\ :1/2),\ -0.525 - 0.850i)

Particular Values

L(1)L(1) == 00
L(12)L(\frac12) == 00
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1+(1+i)T 1 + (1 + i)T
3 1 1
5 1 1
good7 1+(3+3i)T+7iT2 1 + (3 + 3i)T + 7iT^{2}
11 1−11T2 1 - 11T^{2}
13 1+13iT2 1 + 13iT^{2}
17 1−17iT2 1 - 17iT^{2}
19 1+19T2 1 + 19T^{2}
23 1+(1−i)T−23iT2 1 + (1 - i)T - 23iT^{2}
29 1−6iT−29T2 1 - 6iT - 29T^{2}
31 1−31T2 1 - 31T^{2}
37 1−37iT2 1 - 37iT^{2}
41 1+12T+41T2 1 + 12T + 41T^{2}
43 1+(9−9i)T−43iT2 1 + (9 - 9i)T - 43iT^{2}
47 1+(7+7i)T+47iT2 1 + (7 + 7i)T + 47iT^{2}
53 1+53iT2 1 + 53iT^{2}
59 1+59T2 1 + 59T^{2}
61 1+8T+61T2 1 + 8T + 61T^{2}
67 1+(3+3i)T+67iT2 1 + (3 + 3i)T + 67iT^{2}
71 1−71T2 1 - 71T^{2}
73 1+73iT2 1 + 73iT^{2}
79 1+79T2 1 + 79T^{2}
83 1+(11−11i)T−83iT2 1 + (11 - 11i)T - 83iT^{2}
89 1−6iT−89T2 1 - 6iT - 89T^{2}
97 1−97iT2 1 - 97iT^{2}
show more
show less
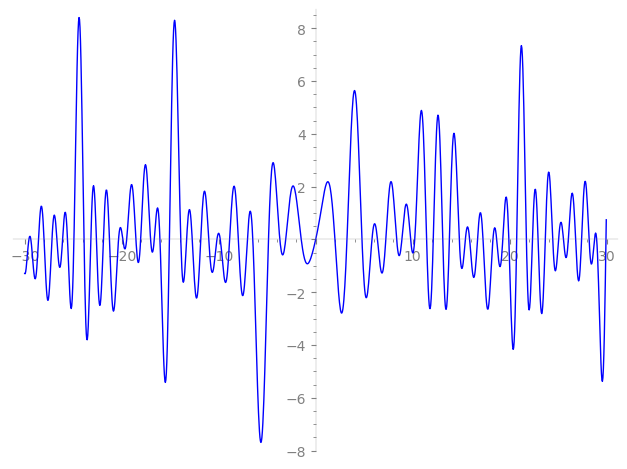
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−9.840646564602905882016952216415, −8.874163464935605254975256118737, −7.980327520811191375411657917353, −7.04592510983331967017197185623, −6.48625854283405323859461544741, −4.86774410197011933552504603467, −3.69955452081662181540677535696, −3.09261678250413111831336110729, −1.49522296593912016389884812796, 0, 1.97857098273931622214722382350, 3.22214226622701215711523678670, 4.76605875059416824221828872885, 5.79875495962519145827089414206, 6.36111142548848000335399366700, 7.22506277653226747992125334886, 8.339160821893038661546252725528, 8.882969361526073725695830923503, 9.783177142889602176615982615267

Graph of the ZZ-function along the critical line