L-function 1-405-405.157-r1-0-0

• Label: 1-405-405.157-r1-0-0
• Degree: $1$
• Conductor: $405$
• Sign: $-0.222 + 0.975i$
• Analytic cond.: $43.5232$
• Root an. cond.: $43.5232$
• Motivic weight: $0$
• Arithmetic: yes
• Rational: no
• Primitive: yes
• Self-dual: no
• Analytic rank: $0$

Dirichlet series

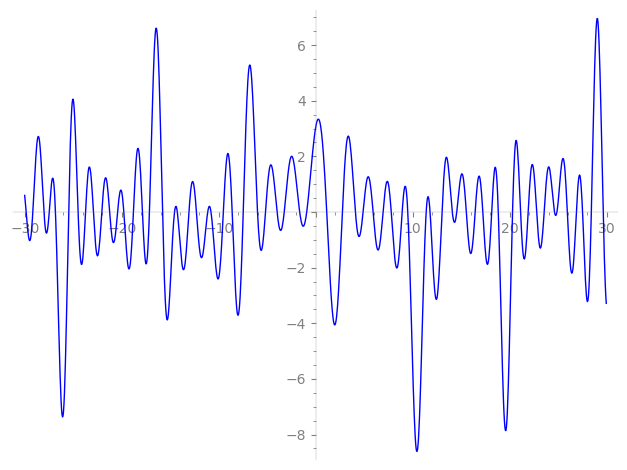
L(s)  = 1

+ (0.448 + 0.893i)2^-s + (−0.597 + 0.802i)4^-s + (0.918 + 0.396i)7^-s + (−0.984 − 0.173i)8^-s + (0.973 + 0.230i)11^-s + (0.549 + 0.835i)13^-s + (0.0581 + 0.998i)14^-s + (−0.286 − 0.957i)16^-s + (0.342 − 0.939i)17^-s + (0.939 − 0.342i)19^-s + (0.230 + 0.973i)22^-s + (0.918 − 0.396i)23^-s + (−0.5 + 0.866i)26^-s + (−0.866 + 0.5i)28^-s + (0.0581 − 0.998i)29^-s + ⋯

Functional equation

$\begin{aligned}\Lambda(s)=\mathstrut & 405 ^{s/2} \, \Gamma_{\R}(s+1) \, L(s)\cr =\mathstrut & (-0.222 + 0.975i)\, \overline{\Lambda}(1-s) \end{aligned}$

Invariants

Degree:	$1$
Conductor:	$405$    =    $3^{4} \cdot 5$
Sign:	$-0.222 + 0.975i$
Analytic conductor:	$43.5232$
Root analytic conductor:	$43.5232$
Motivic weight:	$0$
Rational:	no
Arithmetic:	yes
Character:	$\chi_{405} (157, \cdot )$
Primitive:	yes
Self-dual:	no
Analytic rank:	$0$
Selberg data:	$(1,\ 405,\ (1:\ ),\ -0.222 + 0.975i)$

Particular Values

$L(\frac{1}{2})$	$\approx$	$1.903235012 + 2.385361490i$
$L(1)$	$\approx$	$1.321585226 + 0.8918795715i$

Euler product

   $L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}$

	$p$	$F_p(T)$
bad	3	$1$
	5	$1$
good	2	$1 + (0.448 + 0.893i)T$
	7	$1 + (0.918 + 0.396i)T$
	11	$1 + (0.973 + 0.230i)T$
	13	$1 + (0.549 + 0.835i)T$
	17	$1 + (0.342 - 0.939i)T$
	19	$1 + (0.939 - 0.342i)T$
	23	$1 + (0.918 - 0.396i)T$
	29	$1 + (0.0581 - 0.998i)T$
	31	$1 + (-0.993 - 0.116i)T$

Imaginary part of the first few zeros on the critical line

−23.7256997368704793127271644516, −22.9157664547310643337096951101, −22.05105114436908620429773730793, −21.241635975870125206654482174502, −20.423557716134823258524055673507, −19.78011073723569140674738550981, −18.79139260913617078928769949422, −17.86251764735805503095072669894, −17.142722723549748630617479868542, −15.796167219953215000072594270650, −14.55583568188087203568682104233, −14.26866098396181255854327654986, −13.067422328600059780644860723397, −12.29625809296963884989398512155, −11.13462563816737620076494769782, −10.79330066317575740457537683786, −9.5242239677856388592457947779, −8.61379441089391490983244351600, −7.47217906890890666010048912891, −6.000849138854382651638196896980, −5.17736821340652746368039436867, −3.983325556253383820865338334, −3.24527373132288084983876647234, −1.65296607103442462637869072932, −0.92799652665219963268219076857, 1.13368954687407811887427042868, 2.74405259841490453625342685906, 4.08846384034406110017309535214, 4.88231637820617773603907516005, 5.91229253791907638464248670565, 6.94054227861887027844088625362, 7.78392067303149900823715512610, 8.91084698264302721816338296328, 9.48937360873938660619203986090, 11.38527568531060446039342826802, 11.78551492553335542461032517408, 13.01609956761127254190337829597, 14.0758742401080749528406204442, 14.53867567348668580098993593297, 15.52253920867867399832657898327, 16.43411919556334346969318885875, 17.22360499601273444348262941722, 18.13936810125737522703692258561, 18.81843323730074198516218671417, 20.2881013602629235076987907464, 21.11726306277560775980800179844, 21.89959701665566896328585208392, 22.77229363894549120613295972805, 23.54687696674505643735045665588, 24.61351622877759719633700384512

Graph of the $Z$-function along the critical line