↑

Properties

Label 2-2240-280.69-c0-0-9
Degree $2$
Conductor $2240$
Sign $0.258 + 0.965i$
Analytic cond. $1.11790$
Root an. cond. $1.05731$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + 1.73i·3-s − i·5-s − 7-s − 1.99·9-s − i·11-s − i·13-s + 1.73·15-s − 1.73·17-s − 1.73i·21-s − 25-s − 1.73i·27-s − 1.73i·29-s + 1.73·33-s + i·35-s + 1.73·39-s + ⋯
L(s)  = 1  + 1.73i·3-s − i·5-s − 7-s − 1.99·9-s − i·11-s − i·13-s + 1.73·15-s − 1.73·17-s − 1.73i·21-s − 25-s − 1.73i·27-s − 1.73i·29-s + 1.73·33-s + i·35-s + 1.73·39-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 2240 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.258 + 0.965i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 2240 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.258 + 0.965i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(2240\)    =    \(2^{6} \cdot 5 \cdot 7\)
Sign: $0.258 + 0.965i$
Analytic conductor: \(1.11790\)
Root analytic conductor: \(1.05731\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{2240} (1889, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 2240,\ (\ :0),\ 0.258 + 0.965i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.4873949385\)
\(L(\frac12)\) \(\approx\) \(0.4873949385\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 \)
5 \( 1 + iT \)
7 \( 1 + T \)
good3 \( 1 - 1.73iT - T^{2} \)
11 \( 1 + iT - T^{2} \)
13 \( 1 + iT - T^{2} \)
17 \( 1 + 1.73T + T^{2} \)
19 \( 1 + T^{2} \)
23 \( 1 - T^{2} \)
29 \( 1 + 1.73iT - T^{2} \)
31 \( 1 - T^{2} \)
37 \( 1 + T^{2} \)
41 \( 1 - T^{2} \)
43 \( 1 + T^{2} \)
47 \( 1 + T + T^{2} \)
53 \( 1 + T^{2} \)
59 \( 1 + T^{2} \)
61 \( 1 + T^{2} \)
67 \( 1 + T^{2} \)
71 \( 1 + T^{2} \)
73 \( 1 + T^{2} \)
79 \( 1 + 1.73T + T^{2} \)
83 \( 1 - T^{2} \)
89 \( 1 - T^{2} \)
97 \( 1 - 1.73T + T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

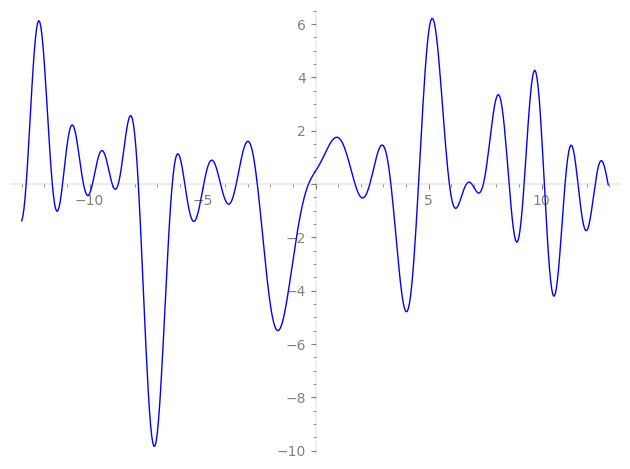
Imaginary part of the first few zeros on the critical line

−8.996296567814500332823160041875, −8.728261001066961559280491741608, −7.84255267468644537602463459269, −6.33964658938566057641234344380, −5.78485833738005751224287080363, −4.94617531358602030327628906473, −4.20238668693489551237951595240, −3.50989590661150073897940972887, −2.57777634615938663534330396823, −0.31024107971170636968755282649, 1.74609745618083056380768413951, 2.40033494539655666440454706602, 3.33178308771758188666261494745, 4.55538815216758117670035557946, 5.92053155975828033261153612143, 6.67442554826816721663465208511, 6.91075002209753406866659732517, 7.42391635808013777773746707013, 8.564647369609327433872337119672, 9.226163090075877818749898909478

Graph of the $Z$-function along the critical line