| L(s) = 1 | + 576.·3-s + 2.27e3·5-s − 3.77e4·7-s + 1.54e5·9-s + 2.14e4·11-s + 1.39e6·13-s + 1.30e6·15-s + 4.72e6·17-s − 1.41e7·19-s − 2.17e7·21-s − 5.42e7·23-s − 4.36e7·25-s − 1.28e7·27-s + 1.55e8·29-s + 1.42e7·31-s + 1.23e7·33-s − 8.56e7·35-s + 4.10e8·37-s + 8.03e8·39-s + 1.58e8·41-s − 1.07e9·43-s + 3.51e8·45-s − 2.52e9·47-s − 5.53e8·49-s + 2.72e9·51-s − 1.99e9·53-s + 4.85e7·55-s + ⋯ |
| L(s) = 1 | + 1.36·3-s + 0.324·5-s − 0.848·7-s + 0.873·9-s + 0.0400·11-s + 1.04·13-s + 0.444·15-s + 0.807·17-s − 1.31·19-s − 1.16·21-s − 1.75·23-s − 0.894·25-s − 0.172·27-s + 1.40·29-s + 0.0892·31-s + 0.0548·33-s − 0.275·35-s + 0.973·37-s + 1.42·39-s + 0.213·41-s − 1.11·43-s + 0.283·45-s − 1.60·47-s − 0.279·49-s + 1.10·51-s − 0.654·53-s + 0.0130·55-s + ⋯ |
\[\begin{aligned}\Lambda(s)=\mathstrut & 256 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & -\, \Lambda(12-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 256 ^{s/2} \, \Gamma_{\C}(s+11/2) \, L(s)\cr =\mathstrut & -\, \Lambda(1-s) \end{aligned}\]
Particular Values
| \(L(6)\) |
\(=\) |
\(0\) |
| \(L(\frac12)\) |
\(=\) |
\(0\) |
| \(L(\frac{13}{2})\) |
|
not available |
| \(L(1)\) |
|
not available |
\(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
| $p$ | $F_p(T)$ |
|---|
| bad | 2 | \( 1 \) |
| good | 3 | \( 1 - 576.T + 1.77e5T^{2} \) |
| 5 | \( 1 - 2.27e3T + 4.88e7T^{2} \) |
| 7 | \( 1 + 3.77e4T + 1.97e9T^{2} \) |
| 11 | \( 1 - 2.14e4T + 2.85e11T^{2} \) |
| 13 | \( 1 - 1.39e6T + 1.79e12T^{2} \) |
| 17 | \( 1 - 4.72e6T + 3.42e13T^{2} \) |
| 19 | \( 1 + 1.41e7T + 1.16e14T^{2} \) |
| 23 | \( 1 + 5.42e7T + 9.52e14T^{2} \) |
| 29 | \( 1 - 1.55e8T + 1.22e16T^{2} \) |
| 31 | \( 1 - 1.42e7T + 2.54e16T^{2} \) |
| 37 | \( 1 - 4.10e8T + 1.77e17T^{2} \) |
| 41 | \( 1 - 1.58e8T + 5.50e17T^{2} \) |
| 43 | \( 1 + 1.07e9T + 9.29e17T^{2} \) |
| 47 | \( 1 + 2.52e9T + 2.47e18T^{2} \) |
| 53 | \( 1 + 1.99e9T + 9.26e18T^{2} \) |
| 59 | \( 1 - 3.21e9T + 3.01e19T^{2} \) |
| 61 | \( 1 - 1.20e10T + 4.35e19T^{2} \) |
| 67 | \( 1 - 4.11e9T + 1.22e20T^{2} \) |
| 71 | \( 1 - 1.02e10T + 2.31e20T^{2} \) |
| 73 | \( 1 + 2.32e10T + 3.13e20T^{2} \) |
| 79 | \( 1 + 3.03e10T + 7.47e20T^{2} \) |
| 83 | \( 1 - 1.08e10T + 1.28e21T^{2} \) |
| 89 | \( 1 + 9.34e10T + 2.77e21T^{2} \) |
| 97 | \( 1 + 1.19e11T + 7.15e21T^{2} \) |
| show more | |
| show less | |
\(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)
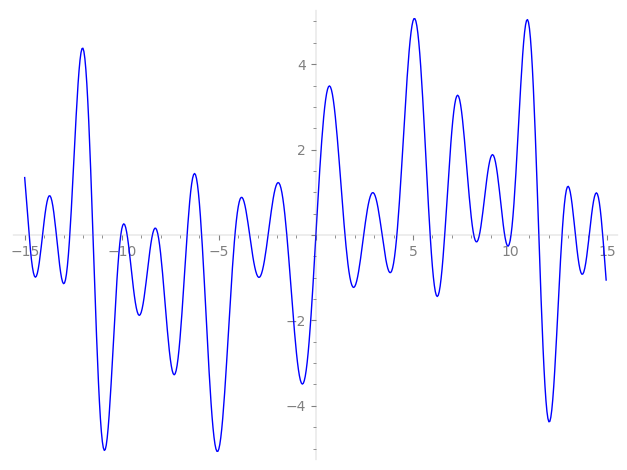
Imaginary part of the first few zeros on the critical line
−9.722683690679871011021840592891, −8.421292071642474493292409495998, −8.131615446704288702355837531949, −6.63464756516365505863641817832, −5.88498266815982643513749674677, −4.17026863692531037415223472262, −3.41095945629728931706651369806, −2.46155758446196605275098592617, −1.49817639827231689913203725001, 0,
1.49817639827231689913203725001, 2.46155758446196605275098592617, 3.41095945629728931706651369806, 4.17026863692531037415223472262, 5.88498266815982643513749674677, 6.63464756516365505863641817832, 8.131615446704288702355837531949, 8.421292071642474493292409495998, 9.722683690679871011021840592891