↑

Properties

Label 2-464-4.3-c2-0-1
Degree 22
Conductor 464464
Sign 0.5−0.866i0.5 - 0.866i
Analytic cond. 12.643012.6430
Root an. cond. 3.555713.55571
Motivic weight 22
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank 00

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

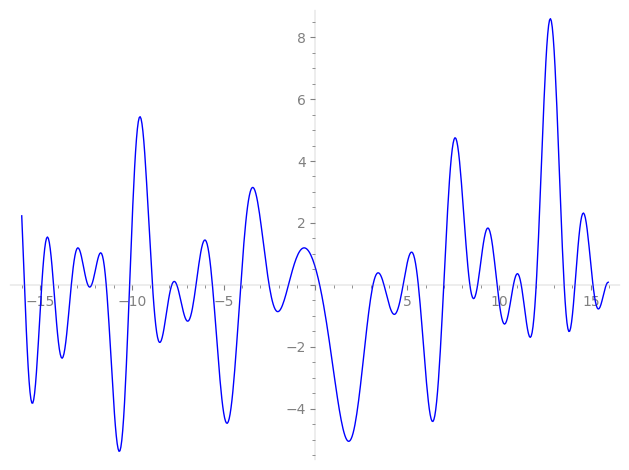
L(s)  = 1  − 5.45i·3-s − 3.94·5-s + 2.61i·7-s − 20.7·9-s + 15.3i·11-s + 1.27·13-s + 21.5i·15-s + 2.27·17-s + 29.0i·19-s + 14.2·21-s − 8.77i·23-s − 9.41·25-s + 64.1i·27-s + 5.38·29-s − 48.1i·31-s + ⋯
L(s)  = 1  − 1.81i·3-s − 0.789·5-s + 0.374i·7-s − 2.30·9-s + 1.39i·11-s + 0.0980·13-s + 1.43i·15-s + 0.133·17-s + 1.52i·19-s + 0.680·21-s − 0.381i·23-s − 0.376·25-s + 2.37i·27-s + 0.185·29-s − 1.55i·31-s + ⋯

Functional equation

Λ(s)=(464s/2 ΓC(s) L(s)=((0.5−0.866i) Λ‾(3−s)\begin{aligned}\Lambda(s)=\mathstrut & 464 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.5 - 0.866i)\, \overline{\Lambda}(3-s) \end{aligned}
Λ(s)=(464s/2 ΓC(s+1) L(s)=((0.5−0.866i) Λ‾(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 464 ^{s/2} \, \Gamma_{\C}(s+1) \, L(s)\cr =\mathstrut & (0.5 - 0.866i)\, \overline{\Lambda}(1-s) \end{aligned}

Invariants

Degree: 22
Conductor: 464464    =    24⋅292^{4} \cdot 29
Sign: 0.5−0.866i0.5 - 0.866i
Analytic conductor: 12.643012.6430
Root analytic conductor: 3.555713.55571
Motivic weight: 22
Rational: no
Arithmetic: yes
Character: χ464(175,⋅)\chi_{464} (175, \cdot )
Primitive: yes
Self-dual: no
Analytic rank: 00
Selberg data: (2, 464, ( :1), 0.5−0.866i)(2,\ 464,\ (\ :1),\ 0.5 - 0.866i)

Particular Values

L(32)L(\frac{3}{2}) ≈\approx 0.54536271210.5453627121
L(12)L(\frac12) ≈\approx 0.54536271210.5453627121
L(2)L(2) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppFp(T)F_p(T)
bad2 1 1
29 1−5.38T 1 - 5.38T
good3 1+5.45iT−9T2 1 + 5.45iT - 9T^{2}
5 1+3.94T+25T2 1 + 3.94T + 25T^{2}
7 1−2.61iT−49T2 1 - 2.61iT - 49T^{2}
11 1−15.3iT−121T2 1 - 15.3iT - 121T^{2}
13 1−1.27T+169T2 1 - 1.27T + 169T^{2}
17 1−2.27T+289T2 1 - 2.27T + 289T^{2}
19 1−29.0iT−361T2 1 - 29.0iT - 361T^{2}
23 1+8.77iT−529T2 1 + 8.77iT - 529T^{2}
31 1+48.1iT−961T2 1 + 48.1iT - 961T^{2}
37 1+54.8T+1.36e3T2 1 + 54.8T + 1.36e3T^{2}
41 1−10.1T+1.68e3T2 1 - 10.1T + 1.68e3T^{2}
43 1+0.0320iT−1.84e3T2 1 + 0.0320iT - 1.84e3T^{2}
47 1−86.1iT−2.20e3T2 1 - 86.1iT - 2.20e3T^{2}
53 1+34.1T+2.80e3T2 1 + 34.1T + 2.80e3T^{2}
59 1−74.2iT−3.48e3T2 1 - 74.2iT - 3.48e3T^{2}
61 1−35.9T+3.72e3T2 1 - 35.9T + 3.72e3T^{2}
67 1−65.2iT−4.48e3T2 1 - 65.2iT - 4.48e3T^{2}
71 1+41.7iT−5.04e3T2 1 + 41.7iT - 5.04e3T^{2}
73 1+105.T+5.32e3T2 1 + 105.T + 5.32e3T^{2}
79 1+40.7iT−6.24e3T2 1 + 40.7iT - 6.24e3T^{2}
83 1−97.7iT−6.88e3T2 1 - 97.7iT - 6.88e3T^{2}
89 1+67.1T+7.92e3T2 1 + 67.1T + 7.92e3T^{2}
97 1+34.9T+9.40e3T2 1 + 34.9T + 9.40e3T^{2}
show more
show less
   L(s)=∏p ∏j=12(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−11.39797400493778386101345113633, −10.12413211180101816223744123416, −8.880202780249424862329559187898, −7.82377728294874823896933448703, −7.55602458753908769586511217159, −6.50574967356126174304337352095, −5.61335761884388530919105886910, −4.06999259133722725640931404169, −2.52506977152778236759171205549, −1.46837136865316426090019115282, 0.22795371246412992413264891489, 3.13515692296242365643761166674, 3.73045938764179470471492532758, 4.77563634985991118500960224751, 5.60264800694926695006897610341, 6.98939454750049952750551133236, 8.410741007203579114175611197887, 8.834101287331649889963223796603, 9.894374272645253739174042603292, 10.78442773039989610005855968803

Graph of the ZZ-function along the critical line