↑

Properties

Label 2-700-28.11-c0-0-1
Degree $2$
Conductor $700$
Sign $-0.553 + 0.832i$
Analytic cond. $0.349345$
Root an. cond. $0.591054$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  + (0.866 − 0.5i)2-s + (−0.866 − 0.5i)3-s + (0.499 − 0.866i)4-s − 0.999·6-s + (−0.866 − 0.5i)7-s − 0.999i·8-s + (−0.866 + 0.499i)12-s − 0.999·14-s + (−0.5 − 0.866i)16-s + (0.499 + 0.866i)21-s + (0.866 − 0.5i)23-s + (−0.499 + 0.866i)24-s + i·27-s + (−0.866 + 0.499i)28-s + 29-s + ⋯
L(s)  = 1  + (0.866 − 0.5i)2-s + (−0.866 − 0.5i)3-s + (0.499 − 0.866i)4-s − 0.999·6-s + (−0.866 − 0.5i)7-s − 0.999i·8-s + (−0.866 + 0.499i)12-s − 0.999·14-s + (−0.5 − 0.866i)16-s + (0.499 + 0.866i)21-s + (0.866 − 0.5i)23-s + (−0.499 + 0.866i)24-s + i·27-s + (−0.866 + 0.499i)28-s + 29-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 700 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.553 + 0.832i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 700 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (-0.553 + 0.832i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(700\)    =    \(2^{2} \cdot 5^{2} \cdot 7\)
Sign: $-0.553 + 0.832i$
Analytic conductor: \(0.349345\)
Root analytic conductor: \(0.591054\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{700} (151, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 700,\ (\ :0),\ -0.553 + 0.832i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.024868594\)
\(L(\frac12)\) \(\approx\) \(1.024868594\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (-0.866 + 0.5i)T \)
5 \( 1 \)
7 \( 1 + (0.866 + 0.5i)T \)
good3 \( 1 + (0.866 + 0.5i)T + (0.5 + 0.866i)T^{2} \)
11 \( 1 + (0.5 + 0.866i)T^{2} \)
13 \( 1 + T^{2} \)
17 \( 1 + (-0.5 - 0.866i)T^{2} \)
19 \( 1 + (0.5 - 0.866i)T^{2} \)
23 \( 1 + (-0.866 + 0.5i)T + (0.5 - 0.866i)T^{2} \)
29 \( 1 - T + T^{2} \)
31 \( 1 + (0.5 + 0.866i)T^{2} \)
37 \( 1 + (-0.5 + 0.866i)T^{2} \)
41 \( 1 + T + T^{2} \)
43 \( 1 - iT - T^{2} \)
47 \( 1 + (-1.73 + i)T + (0.5 - 0.866i)T^{2} \)
53 \( 1 + (-0.5 - 0.866i)T^{2} \)
59 \( 1 + (0.5 + 0.866i)T^{2} \)
61 \( 1 + (-0.5 - 0.866i)T + (-0.5 + 0.866i)T^{2} \)
67 \( 1 + (-0.866 - 0.5i)T + (0.5 + 0.866i)T^{2} \)
71 \( 1 - T^{2} \)
73 \( 1 + (-0.5 - 0.866i)T^{2} \)
79 \( 1 + (0.5 - 0.866i)T^{2} \)
83 \( 1 - iT - T^{2} \)
89 \( 1 + (0.5 + 0.866i)T + (-0.5 + 0.866i)T^{2} \)
97 \( 1 + T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

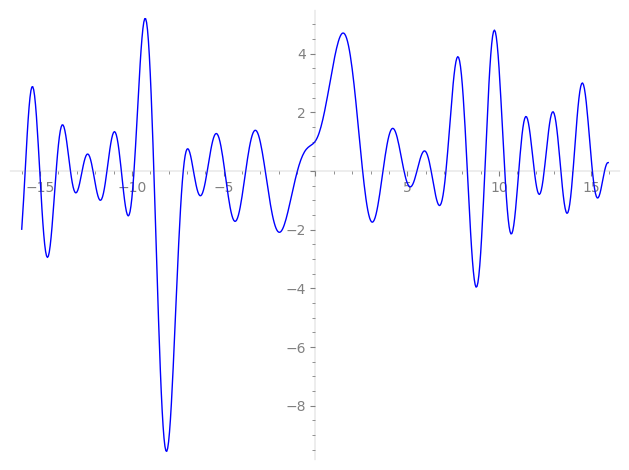
Imaginary part of the first few zeros on the critical line

−10.57394624317188050831943098573, −9.883294561219959206858428489273, −8.802159915662516793696487388050, −7.20237275803542727261896525076, −6.64445824387371851371414029105, −5.89436365706709778425679089108, −4.94059903892542441235336612623, −3.79940559461868676251154183679, −2.73366311502421252743007216621, −0.984672679369739259079610876653, 2.57013339079330267561694860797, 3.67789542204281055769983056446, 4.82484768556985802310350256888, 5.52760340457769480408736273100, 6.30174284513544197052612291144, 7.10872698690888113528102105175, 8.274464093805326766521557867755, 9.226642579717488817866322626041, 10.31102105306279847053213948223, 11.07473173706261922537963971950

Graph of the $Z$-function along the critical line