↑

Properties

Label 2-820-820.403-c0-0-0
Degree $2$
Conductor $820$
Sign $0.884 - 0.466i$
Analytic cond. $0.409233$
Root an. cond. $0.639713$
Motivic weight $0$
Arithmetic yes
Rational no
Primitive yes
Self-dual no
Analytic rank $0$

Origins

Related objects

Downloads

Learn more

Normalization:  

Dirichlet series

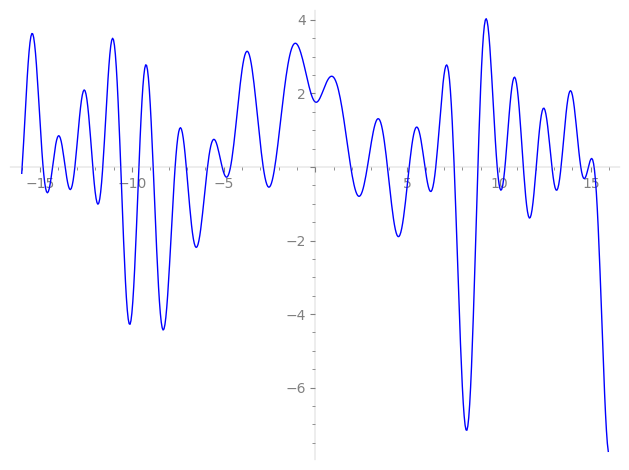
L(s)  = 1  + (0.951 + 0.309i)2-s + (0.809 + 0.587i)4-s + (0.891 − 0.453i)5-s + (0.587 + 0.809i)8-s + (−0.707 + 0.707i)9-s + (0.987 − 0.156i)10-s + (−1.70 + 0.133i)13-s + (0.309 + 0.951i)16-s + (−0.465 − 1.93i)17-s + (−0.891 + 0.453i)18-s + (0.987 + 0.156i)20-s + (0.587 − 0.809i)25-s + (−1.65 − 0.398i)26-s + (−0.652 + 0.399i)29-s + i·32-s + ⋯
L(s)  = 1  + (0.951 + 0.309i)2-s + (0.809 + 0.587i)4-s + (0.891 − 0.453i)5-s + (0.587 + 0.809i)8-s + (−0.707 + 0.707i)9-s + (0.987 − 0.156i)10-s + (−1.70 + 0.133i)13-s + (0.309 + 0.951i)16-s + (−0.465 − 1.93i)17-s + (−0.891 + 0.453i)18-s + (0.987 + 0.156i)20-s + (0.587 − 0.809i)25-s + (−1.65 − 0.398i)26-s + (−0.652 + 0.399i)29-s + i·32-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 820 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.884 - 0.466i)\, \overline{\Lambda}(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 820 ^{s/2} \, \Gamma_{\C}(s) \, L(s)\cr =\mathstrut & (0.884 - 0.466i)\, \overline{\Lambda}(1-s) \end{aligned}\]

Invariants

Degree: \(2\)
Conductor: \(820\)    =    \(2^{2} \cdot 5 \cdot 41\)
Sign: $0.884 - 0.466i$
Analytic conductor: \(0.409233\)
Root analytic conductor: \(0.639713\)
Motivic weight: \(0\)
Rational: no
Arithmetic: yes
Character: $\chi_{820} (403, \cdot )$
Primitive: yes
Self-dual: no
Analytic rank: \(0\)
Selberg data: \((2,\ 820,\ (\ :0),\ 0.884 - 0.466i)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(1.764165935\)
\(L(\frac12)\) \(\approx\) \(1.764165935\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$F_p(T)$
bad2 \( 1 + (-0.951 - 0.309i)T \)
5 \( 1 + (-0.891 + 0.453i)T \)
41 \( 1 + (0.951 + 0.309i)T \)
good3 \( 1 + (0.707 - 0.707i)T^{2} \)
7 \( 1 + (0.156 - 0.987i)T^{2} \)
11 \( 1 + (0.891 - 0.453i)T^{2} \)
13 \( 1 + (1.70 - 0.133i)T + (0.987 - 0.156i)T^{2} \)
17 \( 1 + (0.465 + 1.93i)T + (-0.891 + 0.453i)T^{2} \)
19 \( 1 + (-0.156 + 0.987i)T^{2} \)
23 \( 1 + (0.587 - 0.809i)T^{2} \)
29 \( 1 + (0.652 - 0.399i)T + (0.453 - 0.891i)T^{2} \)
31 \( 1 + (0.309 - 0.951i)T^{2} \)
37 \( 1 + (-1.16 + 0.183i)T + (0.951 - 0.309i)T^{2} \)
43 \( 1 + (0.809 + 0.587i)T^{2} \)
47 \( 1 + (-0.156 - 0.987i)T^{2} \)
53 \( 1 + (-1.26 - 0.303i)T + (0.891 + 0.453i)T^{2} \)
59 \( 1 + (-0.809 - 0.587i)T^{2} \)
61 \( 1 + (0.278 + 0.142i)T + (0.587 + 0.809i)T^{2} \)
67 \( 1 + (-0.453 + 0.891i)T^{2} \)
71 \( 1 + (-0.891 + 0.453i)T^{2} \)
73 \( 1 + 1.97T + T^{2} \)
79 \( 1 + (-0.707 - 0.707i)T^{2} \)
83 \( 1 - iT^{2} \)
89 \( 1 + (-1.84 - 0.144i)T + (0.987 + 0.156i)T^{2} \)
97 \( 1 + (0.243 + 0.398i)T + (-0.453 + 0.891i)T^{2} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{2} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

Imaginary part of the first few zeros on the critical line

−10.60534140686924225230210172433, −9.617490583677095092752040612835, −8.839352857403180271254440199571, −7.64445767631221318197941533858, −7.03608920432862563890404580962, −5.88022342445863992484146836607, −5.08293460131620082574140364525, −4.62706554447727705716843188130, −2.84569026988039599268067648681, −2.21494520710589251224715152495, 1.92236376821973836403390783812, 2.82787762865579891425296423490, 3.92163995766779642830131788382, 5.10651809989965872761109302190, 5.96477763368944218224452867811, 6.55325447524849129514630465555, 7.55749876280028280883146102711, 8.848196484358762008591879625050, 9.900077158430581779960072402003, 10.32176864790115156935984242747

Graph of the $Z$-function along the critical line