↑

Properties

Label 4-14e4-1.1-c2e2-0-1
Degree 44
Conductor 3841638416
Sign 11
Analytic cond. 28.522128.5221
Root an. cond. 2.310972.31097
Motivic weight 22
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

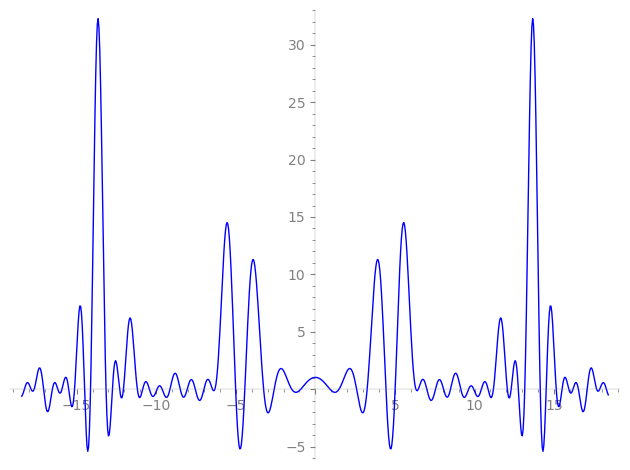
L(s)  = 1  − 4·2-s + 12·4-s − 32·8-s + 18·9-s + 80·16-s − 72·18-s + 48·25-s + 80·29-s − 192·32-s + 216·36-s + 48·37-s − 192·50-s − 180·53-s − 320·58-s + 448·64-s − 576·72-s − 192·74-s + 243·81-s + 576·100-s + 720·106-s − 240·109-s + 60·113-s + 960·116-s + 242·121-s + 127-s − 1.02e3·128-s + 131-s + ⋯
L(s)  = 1  − 2·2-s + 3·4-s − 4·8-s + 2·9-s + 5·16-s − 4·18-s + 1.91·25-s + 2.75·29-s − 6·32-s + 6·36-s + 1.29·37-s − 3.83·50-s − 3.39·53-s − 5.51·58-s + 7·64-s − 8·72-s − 2.59·74-s + 3·81-s + 5.75·100-s + 6.79·106-s − 2.20·109-s + 0.530·113-s + 8.27·116-s + 2·121-s + 0.00787·127-s − 8·128-s + 0.00763·131-s + ⋯

Functional equation

Λ(s)=(38416s/2 ΓC(s)2 L(s)=( Λ(3−s)\begin{aligned}\Lambda(s)=\mathstrut & 38416 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(3-s) \end{aligned}
Λ(s)=(38416s/2 ΓC(s+1)2 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut & 38416 ^{s/2} \, \Gamma_{\C}(s+1)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}

Invariants

Degree: 44
Conductor: 3841638416    =    24⋅742^{4} \cdot 7^{4}
Sign: 11
Analytic conductor: 28.522128.5221
Root analytic conductor: 2.310972.31097
Motivic weight: 22
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (4, 38416, ( :1,1), 1)(4,\ 38416,\ (\ :1, 1),\ 1)

Particular Values

L(32)L(\frac{3}{2}) ≈\approx 1.0389988061.038998806
L(12)L(\frac12) ≈\approx 1.0389988061.038998806
L(2)L(2) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2C1C_1 (1+pT)2 ( 1 + p T )^{2}
7 1 1
good3C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
5C22C_2^2 1−48T2+p4T4 1 - 48 T^{2} + p^{4} T^{4}
11C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
13C22C_2^2 1+240T2+p4T4 1 + 240 T^{2} + p^{4} T^{4}
17C22C_2^2 1+480T2+p4T4 1 + 480 T^{2} + p^{4} T^{4}
19C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
23C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
29C2C_2 (1−40T+p2T2)2 ( 1 - 40 T + p^{2} T^{2} )^{2}
31C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
37C2C_2 (1−24T+p2T2)2 ( 1 - 24 T + p^{2} T^{2} )^{2}
41C22C_2^2 1−1440T2+p4T4 1 - 1440 T^{2} + p^{4} T^{4}
43C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
47C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
53C2C_2 (1+90T+p2T2)2 ( 1 + 90 T + p^{2} T^{2} )^{2}
59C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
61C22C_2^2 1+2640T2+p4T4 1 + 2640 T^{2} + p^{4} T^{4}
67C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
71C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
73C22C_2^2 1+10560T2+p4T4 1 + 10560 T^{2} + p^{4} T^{4}
79C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
83C1C_1×\timesC1C_1 (1−pT)2(1+pT)2 ( 1 - p T )^{2}( 1 + p T )^{2}
89C22C_2^2 1−12480T2+p4T4 1 - 12480 T^{2} + p^{4} T^{4}
97C22C_2^2 1+18720T2+p4T4 1 + 18720 T^{2} + p^{4} T^{4}
show more
show less
   L(s)=∏p ∏j=14(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−12.29957483645858595912604475681, −12.05969426271667443711214752790, −11.18474853293253268510591277637, −10.85105768455747840599779210750, −10.42746641950694823089569663269, −9.950743675716325120434786390903, −9.622660598500276716065877357701, −9.136293817203693786761826685093, −8.488329443821822400870134411587, −8.053895047121480890664567163296, −7.54349624694807677832046655208, −7.00447162039958653641435196975, −6.46172645210458395389368768624, −6.31689026847130285081656716190, −5.01109808819709229740684019061, −4.43368957224282451476608778247, −3.25167887480955866489941193263, −2.59062794112887481138031594308, −1.48040477790964852118698579886, −0.923520418246340148554936793549, 0.923520418246340148554936793549, 1.48040477790964852118698579886, 2.59062794112887481138031594308, 3.25167887480955866489941193263, 4.43368957224282451476608778247, 5.01109808819709229740684019061, 6.31689026847130285081656716190, 6.46172645210458395389368768624, 7.00447162039958653641435196975, 7.54349624694807677832046655208, 8.053895047121480890664567163296, 8.488329443821822400870134411587, 9.136293817203693786761826685093, 9.622660598500276716065877357701, 9.950743675716325120434786390903, 10.42746641950694823089569663269, 10.85105768455747840599779210750, 11.18474853293253268510591277637, 12.05969426271667443711214752790, 12.29957483645858595912604475681

Graph of the ZZ-function along the critical line