↑

Properties

Label 4-2028e2-1.1-c0e2-0-2
Degree $4$
Conductor $4112784$
Sign $1$
Analytic cond. $1.02435$
Root an. cond. $1.00603$
Motivic weight $0$
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank $0$

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

L(s)  = 1  − 2·2-s + 3·4-s − 2·5-s − 4·8-s − 9-s + 4·10-s + 2·11-s + 5·16-s + 2·18-s − 6·20-s − 4·22-s + 2·25-s − 6·32-s − 3·36-s + 8·40-s + 2·41-s + 6·44-s + 2·45-s + 2·47-s − 4·50-s − 4·55-s + 2·59-s + 7·64-s + 2·71-s + 4·72-s − 10·80-s + 81-s + ⋯
L(s)  = 1  − 2·2-s + 3·4-s − 2·5-s − 4·8-s − 9-s + 4·10-s + 2·11-s + 5·16-s + 2·18-s − 6·20-s − 4·22-s + 2·25-s − 6·32-s − 3·36-s + 8·40-s + 2·41-s + 6·44-s + 2·45-s + 2·47-s − 4·50-s − 4·55-s + 2·59-s + 7·64-s + 2·71-s + 4·72-s − 10·80-s + 81-s + ⋯

Functional equation

\[\begin{aligned}\Lambda(s)=\mathstrut & 4112784 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]
\[\begin{aligned}\Lambda(s)=\mathstrut & 4112784 ^{s/2} \, \Gamma_{\C}(s)^{2} \, L(s)\cr =\mathstrut & \, \Lambda(1-s) \end{aligned}\]

Invariants

Degree: \(4\)
Conductor: \(4112784\)    =    \(2^{4} \cdot 3^{2} \cdot 13^{4}\)
Sign: $1$
Analytic conductor: \(1.02435\)
Root analytic conductor: \(1.00603\)
Motivic weight: \(0\)
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: \(0\)
Selberg data: \((4,\ 4112784,\ (\ :0, 0),\ 1)\)

Particular Values

\(L(\frac{1}{2})\) \(\approx\) \(0.3304822112\)
\(L(\frac12)\) \(\approx\) \(0.3304822112\)
\(L(1)\) not available
\(L(1)\) not available

Euler product

   \(L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1} \)
$p$$\Gal(F_p)$$F_p(T)$
bad2$C_1$ \( ( 1 + T )^{2} \)
3$C_2$ \( 1 + T^{2} \)
13 \( 1 \)
good5$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
7$C_2^2$ \( 1 + T^{4} \)
11$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
17$C_2$ \( ( 1 + T^{2} )^{2} \)
19$C_2^2$ \( 1 + T^{4} \)
23$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
29$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
31$C_2^2$ \( 1 + T^{4} \)
37$C_2^2$ \( 1 + T^{4} \)
41$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
43$C_2$ \( ( 1 + T^{2} )^{2} \)
47$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
53$C_1$$\times$$C_1$ \( ( 1 - T )^{2}( 1 + T )^{2} \)
59$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
61$C_2$ \( ( 1 + T^{2} )^{2} \)
67$C_2^2$ \( 1 + T^{4} \)
71$C_1$$\times$$C_2$ \( ( 1 - T )^{2}( 1 + T^{2} ) \)
73$C_2^2$ \( 1 + T^{4} \)
79$C_2$ \( ( 1 + T^{2} )^{2} \)
83$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
89$C_1$$\times$$C_2$ \( ( 1 + T )^{2}( 1 + T^{2} ) \)
97$C_2^2$ \( 1 + T^{4} \)
show more
show less
   \(L(s) = \displaystyle\prod_p \ \prod_{j=1}^{4} (1 - \alpha_{j,p}\, p^{-s})^{-1}\)

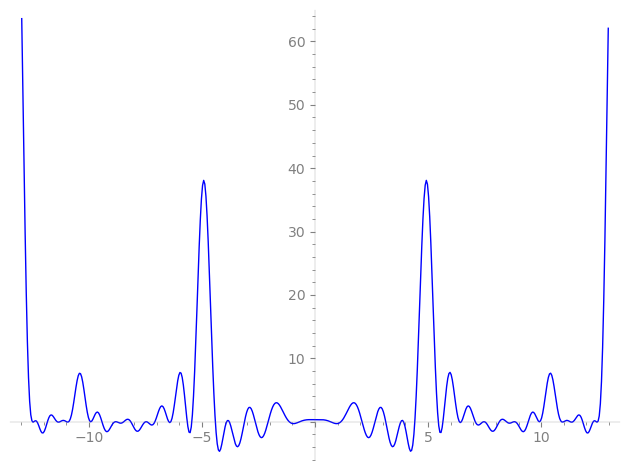
Imaginary part of the first few zeros on the critical line

−9.429175970839669992314016320493, −8.844411680549665924755941856157, −8.788311079053535587231515379599, −8.466576564368633891575538956094, −8.152524119260823843322354538919, −7.49459206035581429032282318774, −7.45100208269666008629506502182, −7.08787643542006332680443736993, −6.47245280326769663830592376429, −6.38367174198439832934284263040, −5.65647216135132157282707735115, −5.45313388208230079270890482121, −4.41201995288830945696042840231, −3.91394188591685008002032078162, −3.79452005981392926041927245158, −3.12557753267479880337052821483, −2.64911719924869438233920884333, −2.07769305522838036469947486518, −1.14134639604706353862457351261, −0.68281756649636679151848371362, 0.68281756649636679151848371362, 1.14134639604706353862457351261, 2.07769305522838036469947486518, 2.64911719924869438233920884333, 3.12557753267479880337052821483, 3.79452005981392926041927245158, 3.91394188591685008002032078162, 4.41201995288830945696042840231, 5.45313388208230079270890482121, 5.65647216135132157282707735115, 6.38367174198439832934284263040, 6.47245280326769663830592376429, 7.08787643542006332680443736993, 7.45100208269666008629506502182, 7.49459206035581429032282318774, 8.152524119260823843322354538919, 8.466576564368633891575538956094, 8.788311079053535587231515379599, 8.844411680549665924755941856157, 9.429175970839669992314016320493

Graph of the $Z$-function along the critical line