↑

Properties

Label 8-1920e4-1.1-c1e4-0-28
Degree 88
Conductor 135895.450×108135895.450\times 10^{8}
Sign 11
Analytic cond. 55247.555247.5
Root an. cond. 3.915513.91551
Motivic weight 11
Arithmetic yes
Rational yes
Primitive no
Self-dual yes
Analytic rank 00

Origins

Origins of factors

Downloads

Learn more

Normalization:  

Dirichlet series

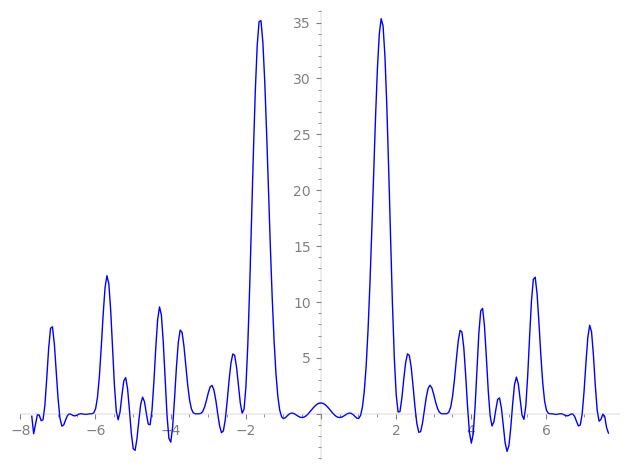
L(s)  = 1  − 2·3-s − 12·7-s + 2·9-s + 24·21-s + 10·25-s − 6·27-s + 24·29-s + 72·49-s − 24·63-s − 20·75-s + 11·81-s + 44·83-s − 48·87-s + 72·101-s + 36·103-s − 52·107-s + 44·121-s + 127-s + 131-s + 137-s + 139-s − 144·147-s + 149-s + 151-s + 157-s + 163-s + 167-s + ⋯
L(s)  = 1  − 1.15·3-s − 4.53·7-s + 2/3·9-s + 5.23·21-s + 2·25-s − 1.15·27-s + 4.45·29-s + 72/7·49-s − 3.02·63-s − 2.30·75-s + 11/9·81-s + 4.82·83-s − 5.14·87-s + 7.16·101-s + 3.54·103-s − 5.02·107-s + 4·121-s + 0.0887·127-s + 0.0873·131-s + 0.0854·137-s + 0.0848·139-s − 11.8·147-s + 0.0819·149-s + 0.0813·151-s + 0.0798·157-s + 0.0783·163-s + 0.0773·167-s + ⋯

Functional equation

Λ(s)=((228⋅34⋅54)s/2 ΓC(s)4 L(s)=( Λ(2−s)\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{28} \cdot 3^{4} \cdot 5^{4}\right)^{s/2} \, \Gamma_{\C}(s)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(2-s)\end{aligned}
Λ(s)=((228⋅34⋅54)s/2 ΓC(s+1/2)4 L(s)=( Λ(1−s)\begin{aligned}\Lambda(s)=\mathstrut &\left(2^{28} \cdot 3^{4} \cdot 5^{4}\right)^{s/2} \, \Gamma_{\C}(s+1/2)^{4} \, L(s)\cr=\mathstrut & \,\Lambda(1-s)\end{aligned}

Invariants

Degree: 88
Conductor: 228⋅34⋅542^{28} \cdot 3^{4} \cdot 5^{4}
Sign: 11
Analytic conductor: 55247.555247.5
Root analytic conductor: 3.915513.91551
Motivic weight: 11
Rational: yes
Arithmetic: yes
Character: Trivial
Primitive: no
Self-dual: yes
Analytic rank: 00
Selberg data: (8, 228⋅34⋅54, ( :1/2,1/2,1/2,1/2), 1)(8,\ 2^{28} \cdot 3^{4} \cdot 5^{4} ,\ ( \ : 1/2, 1/2, 1/2, 1/2 ),\ 1 )

Particular Values

L(1)L(1) ≈\approx 0.97185380660.9718538066
L(12)L(\frac12) ≈\approx 0.97185380660.9718538066
L(32)L(\frac{3}{2}) not available
L(1)L(1) not available

Euler product

   L(s)=∏pFp(p−s)−1L(s) = \displaystyle \prod_{p} F_p(p^{-s})^{-1}
ppGal⁡(Fp)\Gal(F_p)Fp(T)F_p(T)
bad2 1 1
3C22C_2^2 1+2T+2T2+2pT3+p2T4 1 + 2 T + 2 T^{2} + 2 p T^{3} + p^{2} T^{4}
5C2C_2 (1−pT2)2 ( 1 - p T^{2} )^{2}
good7C22C_2^2 (1+6T+18T2+6pT3+p2T4)2 ( 1 + 6 T + 18 T^{2} + 6 p T^{3} + p^{2} T^{4} )^{2}
11C2C_2 (1−pT2)4 ( 1 - p T^{2} )^{4}
13C2C_2 (1+pT2)4 ( 1 + p T^{2} )^{4}
17C2C_2 (1+pT2)4 ( 1 + p T^{2} )^{4}
19C2C_2 (1+pT2)4 ( 1 + p T^{2} )^{4}
23C22C_2^2×\timesC22C_2^2 (1−2T+2T2−2pT3+p2T4)(1+2T+2T2+2pT3+p2T4) ( 1 - 2 T + 2 T^{2} - 2 p T^{3} + p^{2} T^{4} )( 1 + 2 T + 2 T^{2} + 2 p T^{3} + p^{2} T^{4} )
29C2C_2 (1−6T+pT2)4 ( 1 - 6 T + p T^{2} )^{4}
31C2C_2 (1−pT2)4 ( 1 - p T^{2} )^{4}
37C2C_2 (1+pT2)4 ( 1 + p T^{2} )^{4}
41C22C_2^2 (1+62T2+p2T4)2 ( 1 + 62 T^{2} + p^{2} T^{4} )^{2}
43C22C_2^2×\timesC22C_2^2 (1−18T+162T2−18pT3+p2T4)(1+18T+162T2+18pT3+p2T4) ( 1 - 18 T + 162 T^{2} - 18 p T^{3} + p^{2} T^{4} )( 1 + 18 T + 162 T^{2} + 18 p T^{3} + p^{2} T^{4} )
47C22C_2^2×\timesC22C_2^2 (1−14T+98T2−14pT3+p2T4)(1+14T+98T2+14pT3+p2T4) ( 1 - 14 T + 98 T^{2} - 14 p T^{3} + p^{2} T^{4} )( 1 + 14 T + 98 T^{2} + 14 p T^{3} + p^{2} T^{4} )
53C2C_2 (1−pT2)4 ( 1 - p T^{2} )^{4}
59C2C_2 (1−pT2)4 ( 1 - p T^{2} )^{4}
61C22C_2^2 (1−58T2+p2T4)2 ( 1 - 58 T^{2} + p^{2} T^{4} )^{2}
67C22C_2^2×\timesC22C_2^2 (1−6T+18T2−6pT3+p2T4)(1+6T+18T2+6pT3+p2T4) ( 1 - 6 T + 18 T^{2} - 6 p T^{3} + p^{2} T^{4} )( 1 + 6 T + 18 T^{2} + 6 p T^{3} + p^{2} T^{4} )
71C2C_2 (1+pT2)4 ( 1 + p T^{2} )^{4}
73C2C_2 (1−pT2)4 ( 1 - p T^{2} )^{4}
79C2C_2 (1−pT2)4 ( 1 - p T^{2} )^{4}
83C22C_2^2 (1−22T+242T2−22pT3+p2T4)2 ( 1 - 22 T + 242 T^{2} - 22 p T^{3} + p^{2} T^{4} )^{2}
89C2C_2 (1−6T+pT2)2(1+6T+pT2)2 ( 1 - 6 T + p T^{2} )^{2}( 1 + 6 T + p T^{2} )^{2}
97C2C_2 (1−pT2)4 ( 1 - p T^{2} )^{4}
show more
show less
   L(s)=∏p ∏j=18(1−αj,p p−s)−1L(s) = \displaystyle\prod_p \ \prod_{j=1}^{8} (1 - \alpha_{j,p}\, p^{-s})^{-1}

Imaginary part of the first few zeros on the critical line

−6.41107655812277498565487239646, −6.36251399546116178535706637469, −6.14661796493126773161628836506, −6.10873500084234415115075507025, −6.09605387708813105993272224185, −5.43591226437249346217464617614, −5.35084272240477023762877683464, −5.08594753628017057861796356629, −4.82499018857933670360990128283, −4.64221672376206259379062627607, −4.50169762663541716834269026783, −4.09567646597640512895996247776, −3.91808875249130013207707724221, −3.34431769883903162803898894090, −3.30025837259237129324122759116, −3.25812768095409162703779132147, −3.23747753694142801973158741297, −2.74350528394313331854383477052, −2.52506338656078348156080828548, −2.08059419352610335641479018500, −2.07863211689048382151470132373, −1.07180392675020249819394692854, −0.830386226316714201500292802031, −0.70435770903023683861291531643, −0.33406559510895863014558709123, 0.33406559510895863014558709123, 0.70435770903023683861291531643, 0.830386226316714201500292802031, 1.07180392675020249819394692854, 2.07863211689048382151470132373, 2.08059419352610335641479018500, 2.52506338656078348156080828548, 2.74350528394313331854383477052, 3.23747753694142801973158741297, 3.25812768095409162703779132147, 3.30025837259237129324122759116, 3.34431769883903162803898894090, 3.91808875249130013207707724221, 4.09567646597640512895996247776, 4.50169762663541716834269026783, 4.64221672376206259379062627607, 4.82499018857933670360990128283, 5.08594753628017057861796356629, 5.35084272240477023762877683464, 5.43591226437249346217464617614, 6.09605387708813105993272224185, 6.10873500084234415115075507025, 6.14661796493126773161628836506, 6.36251399546116178535706637469, 6.41107655812277498565487239646

Graph of the ZZ-function along the critical line